25年电赛小黑屋，再战VCO¶

约 2386 个字预计阅读时间 13 分钟

写在前面¶

电赛小黑屋告一段落，但抱憾于后半部分的压控方波振荡器，也希望借这个机会再复习一下模电基础知识，故写下此文

题目背景

前面的四二编码与DAC四电平输出不再赘述，直接从VCO的工作原理开始

给入0.8、1.6、2.4、3.2V四个电平，要求输出频率不低于1KHz，且频率间隔不小于500Hz的方波信号，占空比连续可调，幅值尽可能大
5V双电源，限制有源芯片（LM324还剩下三个运放，74LS00还有俩与非门）
自带提示:可通过积分电路与施密特触发器构建VCO

小黑屋期间，我们的大致方案是：积分电路反向输入端直接馈入控制电平，通过增加\(u_{in}\)来提高三角波频率，再通过施密特触发器输出方波信号，通过二极管反馈到反向输入端，希望形成幅值为\(U_{ref}\)的方波。最后，引出三角波进单限比较器即可实现大幅度占空比可调方波

经过几个小时的小黑屋垂死挣扎，我们悬着的心终于在秒针划过下午三点的那一刻死了🥲

反思一下，还是基础不够扎实，知其然而不知其所以然，于是题目一变不能直接套模板，动作就变形了

具体来说，此前的问题集中在电平控制方式上。换句话说，是我们因没有充分理解积分电路而Take it for granted，引发了最后的悲剧

实际上，我们不能直接馈入一个正向的电压，而应该是反向的电流,后面我会解释为什么

所以，我们需要先重拾积分电路的实现原理，这是问题的关键

你好，积分电路¶

对于任何一个带有运放的电路，虚断虚短分析是躲不掉滴

题外话

虚断是运放高输入阻抗带来的特性，是放之四海而皆准的真理

而虚短本质上是其同向/反向输入端在线性放大区的\(\Delta U\)很小的性质带来的近似相等，故只可在负反馈工作模式下分析

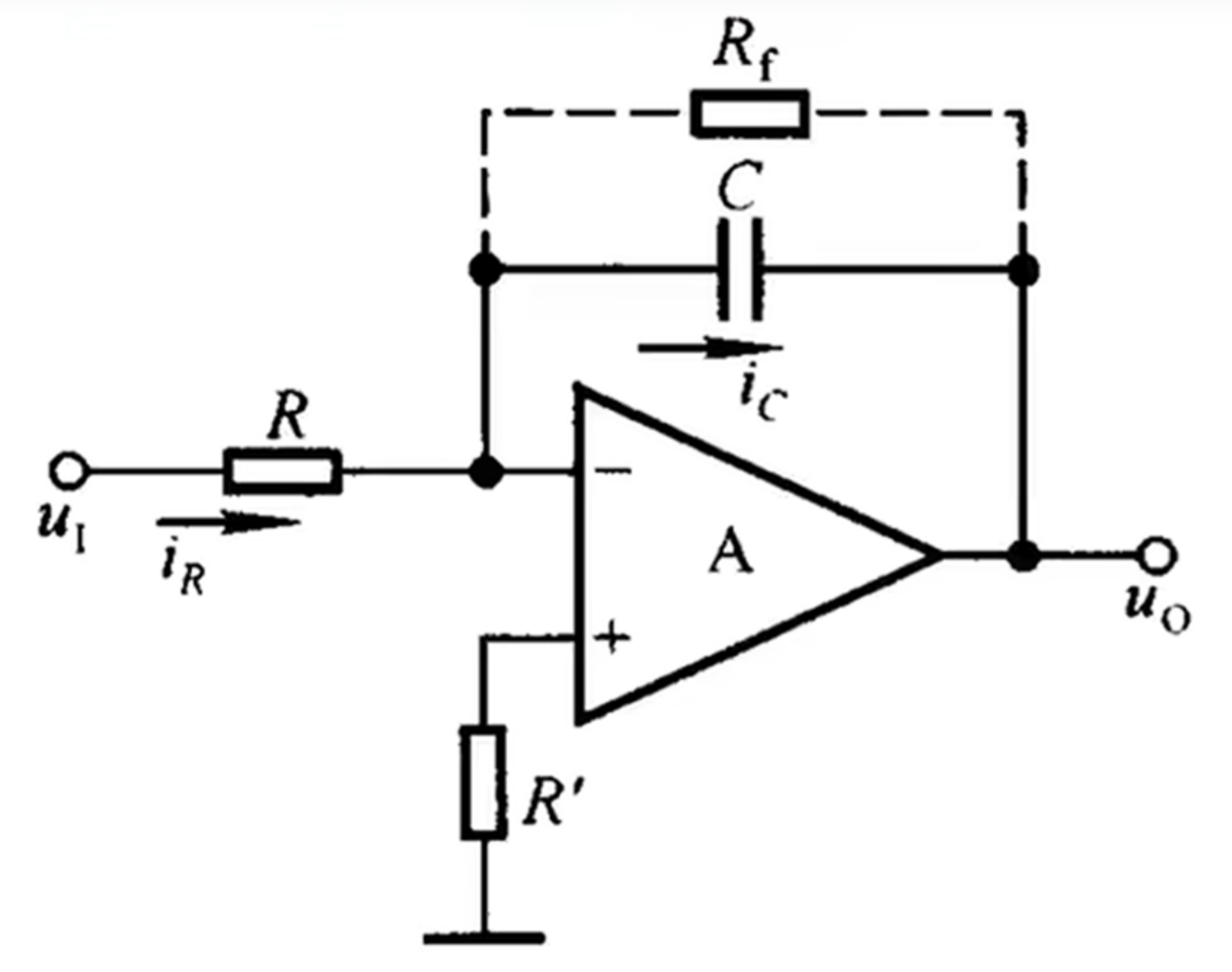
先从一个标准的反向积分电路出发，抄一抄教材：

通过虚短虚断，我们可以得到

\[ u_n=u_p=0 \quad i_{c}=i_{R}=\frac{u_{i}}{R} \]

注意参考方向，又有

\[ u_o = -u_c \]

结合电容电流计算公式

\[ i_c=C\frac{du_{c}}{dt} = -C\frac{du_{o}}{dt} \]

带掉\(i_c\)，两边积分得

\[ u_o=-\frac{1}{RC}\int_{t_0}^{t_1}u_idt + u_0(t_0) \]

当输入电压为电平值时，积分可简化为

\[ u_o=-\frac{1}{RC}U_i\cdot \Delta t +u_0(t_0) \]

所以，充放电速度取决于\(\tau = RC\)和电平大小

这里的时间由输入信号的频率决定，在这里受施密特触发器门限控制

从上式中，我们不难注意到两个对于考试来说无足轻重，但在实际项目中则必须纳入考量的问题：

并联的反馈电阻作用与选择
单电源信号输入的偏置考量

WHY 反馈电阻？¶

反馈电阻在大多数情况是必要，因为所有的运放都带有偏置电流和失调电压，在大幅度积分时容易让电容一直充电，导致输出漂移到轨

精密小信号运放也许不需要考虑这个问题

给出结论，反馈电阻的作用如下：

抑制直流漂移。为运放的输入偏置电流 \(I_b\) 和失调电压\(V_{os}\) 提供直流泄放路径
稳定输出，设定偏置。将积分器的直流增益限制为有限值\(\frac{R_f}{R}\) ，避免积分器成为开环放大器

需要注意:

反馈电阻引入额外的相位，这需要调整电容C来适应项目
\(R_f >> R\)，实际积分有效频率为\(f>>\frac{1}{2\pi R_fC}\)，所以反馈电阻应足够大

偏置是一门艺术¶

先让我们康康一个典型的demo（GIF）

改变偏置后的积分结果

令输入为一个直流方波信号，随着偏置点的变大，三角波像是和土里长出来一样，最后顶到3.5V的运放饱和电压上

有意思的是，若你把反馈电阻去掉，就能直观感受到漂移的力量🤪

双电源自然无需考虑这一点，但大多情况下，单电源的约束迫使我们正视搞懂背后的原理

让我们重新审视电路。令反向输入端电阻为\(R\),反馈电阻为\(R_f\)
根据KCL，有

\[ i_{R}+i_{C}+i_{Rf}=0 \]

妙妙展开

\[ \frac{u_i(t)-U_{ref}}{R}+\frac{u_o(t)-U_{ref}}{R_{f}}+C\frac{du_o(t)}{dt}=0 \]

整理为一阶线性微分方程的形式

\[ R_{f}C\cdot u_o'(t)+u_o(t)=-\frac{R_{f}}{R}(u_i(t)-U_{ref})+U_{ref} \]

关注直流分量的稳态解，输入 \(u_i(t)\) 取其平均值 \(U_{iavg}\)，则有

\[ 0+U_{odc}=-\frac{R_{f}}{R}(U_{iavg}-U_{ref})+U_{ref} \]

假设增益比为5，对于当前情况有

\[ U_{odc}=-5(2.5V-2.5V)+2.5V=2.5V \]

这证明了电路的稳态输出中心电压是 2.5V

再着眼于齐次解，不难发现其解为指数形式

\[ u_{oh}(t) = A \cdot e^{-t/\tau} = A \cdot e^{-t/R_fC} \]

得到通解，并代入初始电压为0的条件解出A，最终得到

\[ u_{o}(t)=2.5 \cdot(1-e^{-t/\tau}) \]

所以，我们发现直流信号会逐渐收敛于一个值，而三角波会在其附近震荡

最后，让我们看看，如果偏置是其他值而非均值，又会发生什么：

\[ U_{odc}=-G(U_{iavg}-U_{ref})+U_{ref} \]

现在，稳态直流量不再是\(U_{ref}\)，还要加上一个非零线性项

若增益大于1，则一点点的偏差都会被放大，导致三角波顶到轨而失真

结论

对于一个带偏置与占空比的方波，你需要尽可能让运放偏置等于其均值

再战VCO¶

在确定基于74LS00的与非门生成TTL方波后，随后需要注意的就是2.5V的运放偏置。但单纯的信号发生器仍不能满足要求，电平控制方案仍是关键

需要注意的是，此时的方波高电平已经顶到运放饱和电压，所以再增加电平是没有意义的；相反，应该在固有震荡的频率的基础上，控制降低其频率

又因为运放压控的本质是控制其电流，即回到一开始的KCL方程（为简化讨论，这里不考虑偏置的问题）：

\[ i_c=i_R=\frac{u_i}{R} \rightarrow u_o = -\frac{1}{C}\int i_R dt + u_0 \]

RC固定，那么唯一可控的变量就是电流。不妨再馈入一路反向电流，使得

\[ i_R' = i_R - i_{Control} \]

进而控制锯齿波频率

这里说的是锯齿波而非三角波，是因为电流的减少，对于已经位于0V低电平（放电；三角波的上升过程）来说，是不起作用的
它只会让充电时间变慢，故占空比的不同表现为锯齿波~

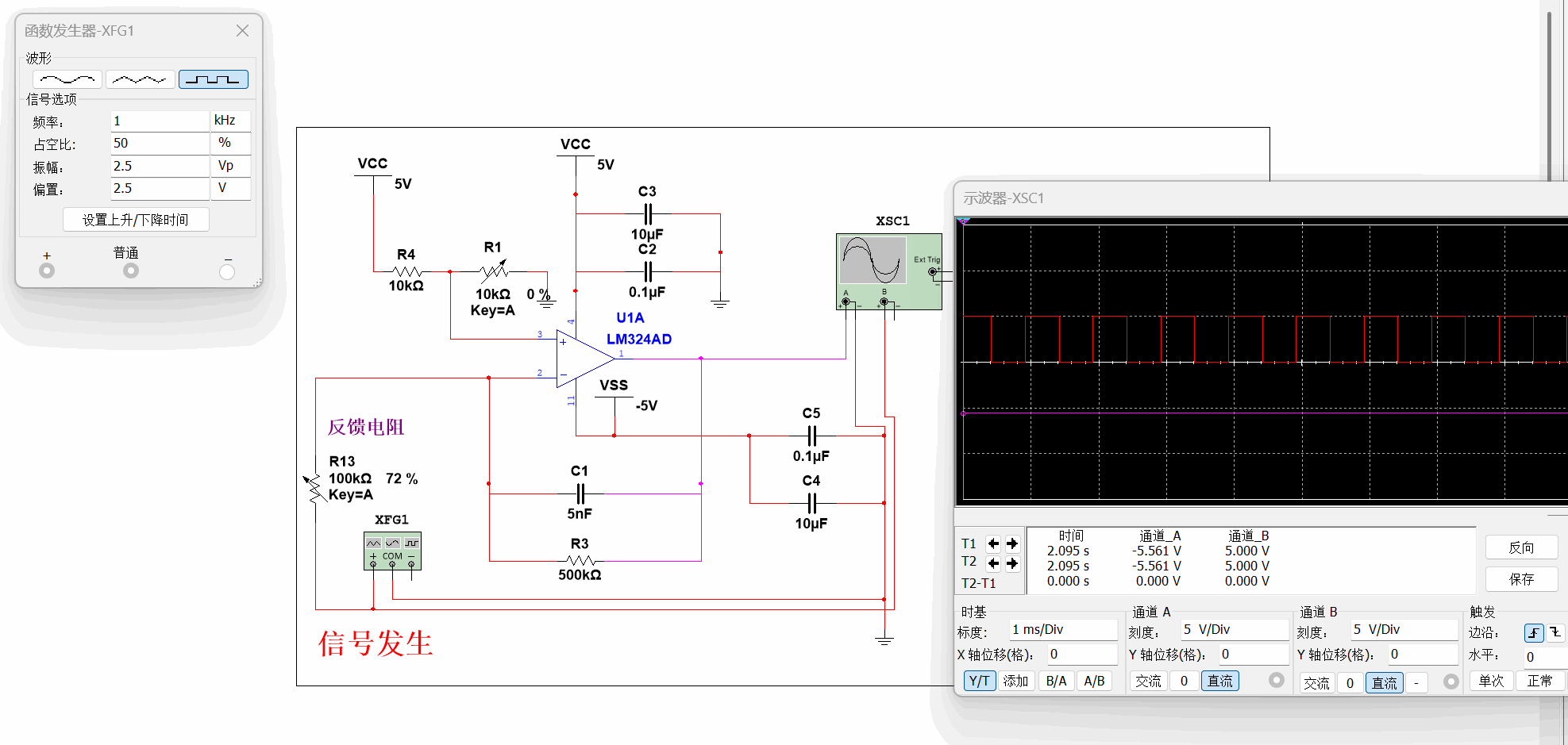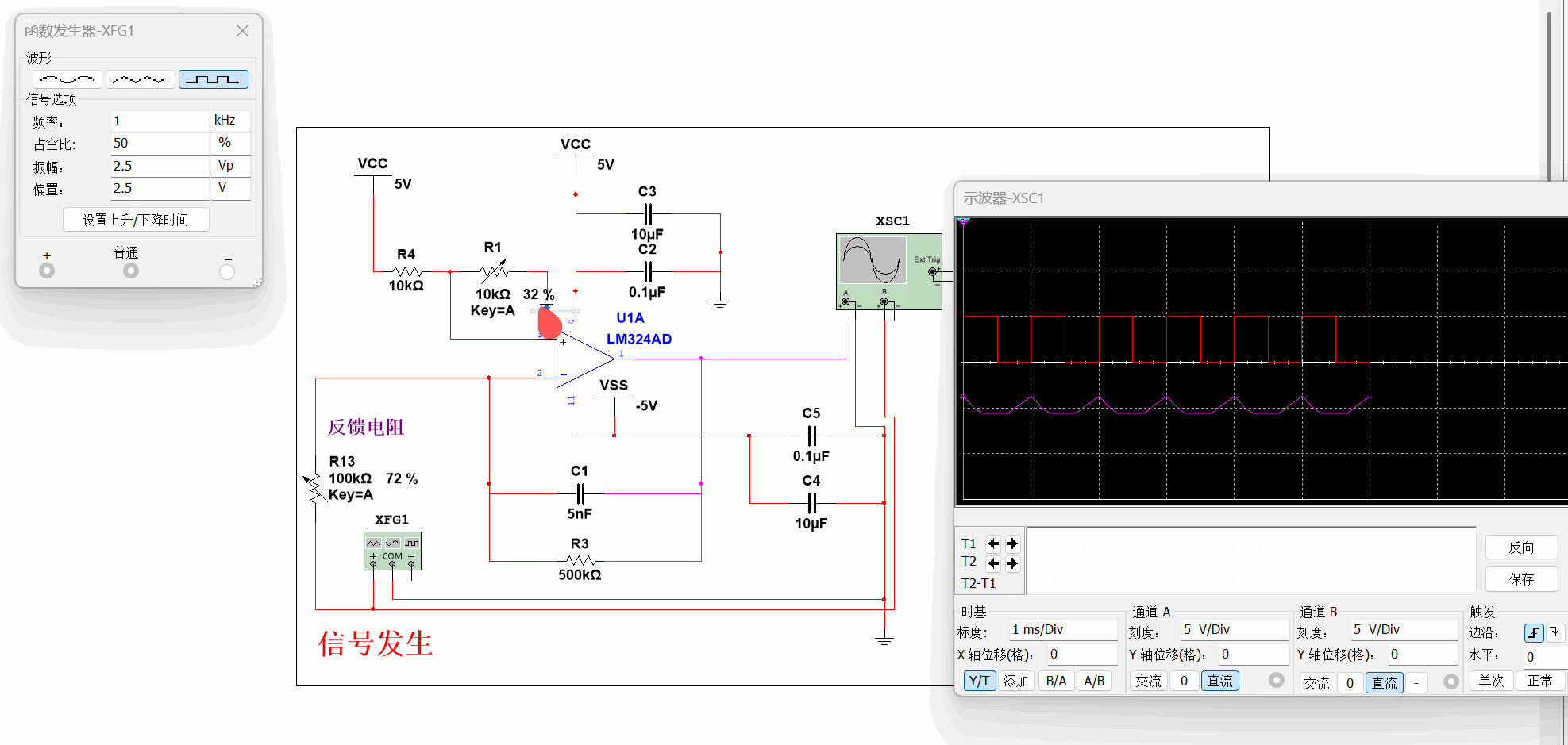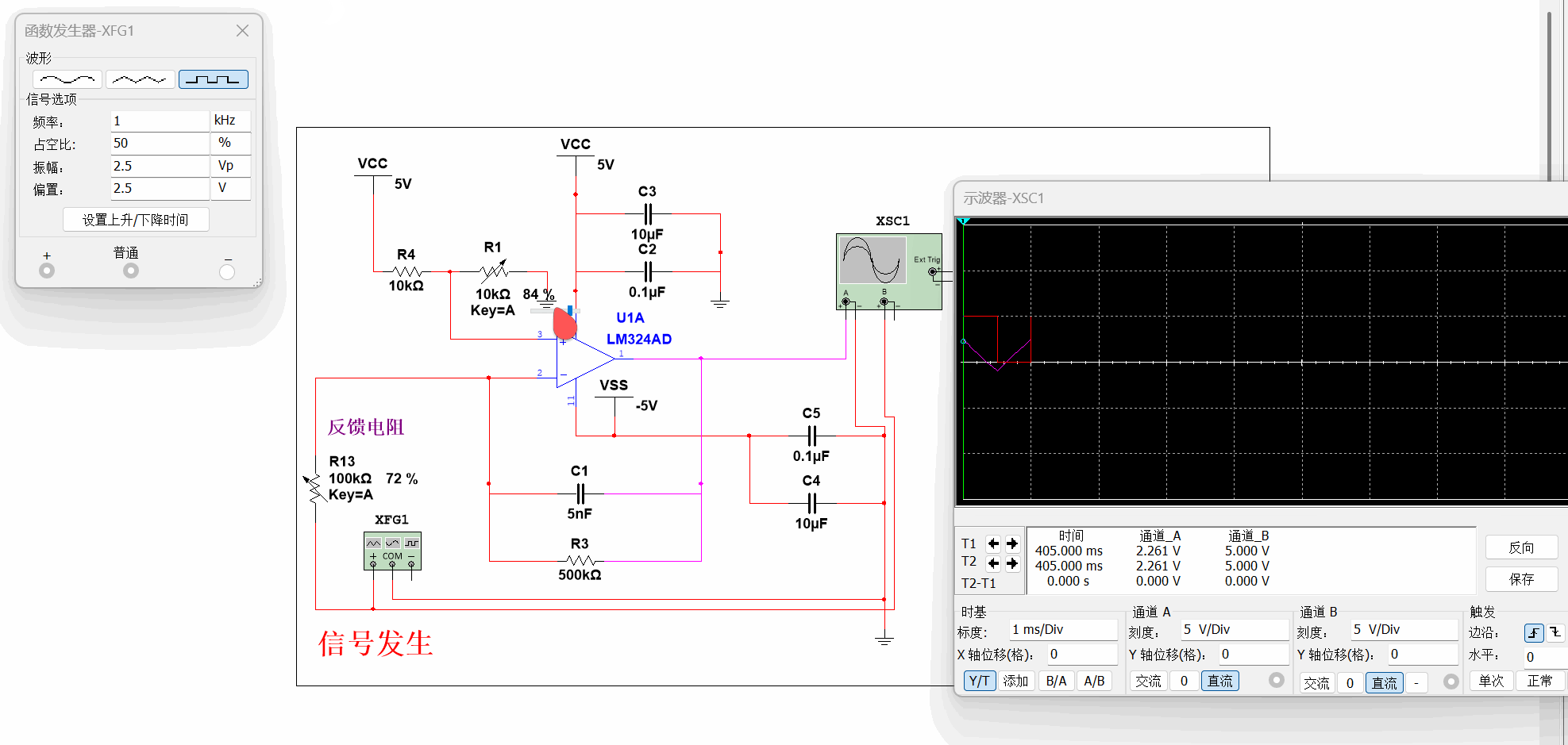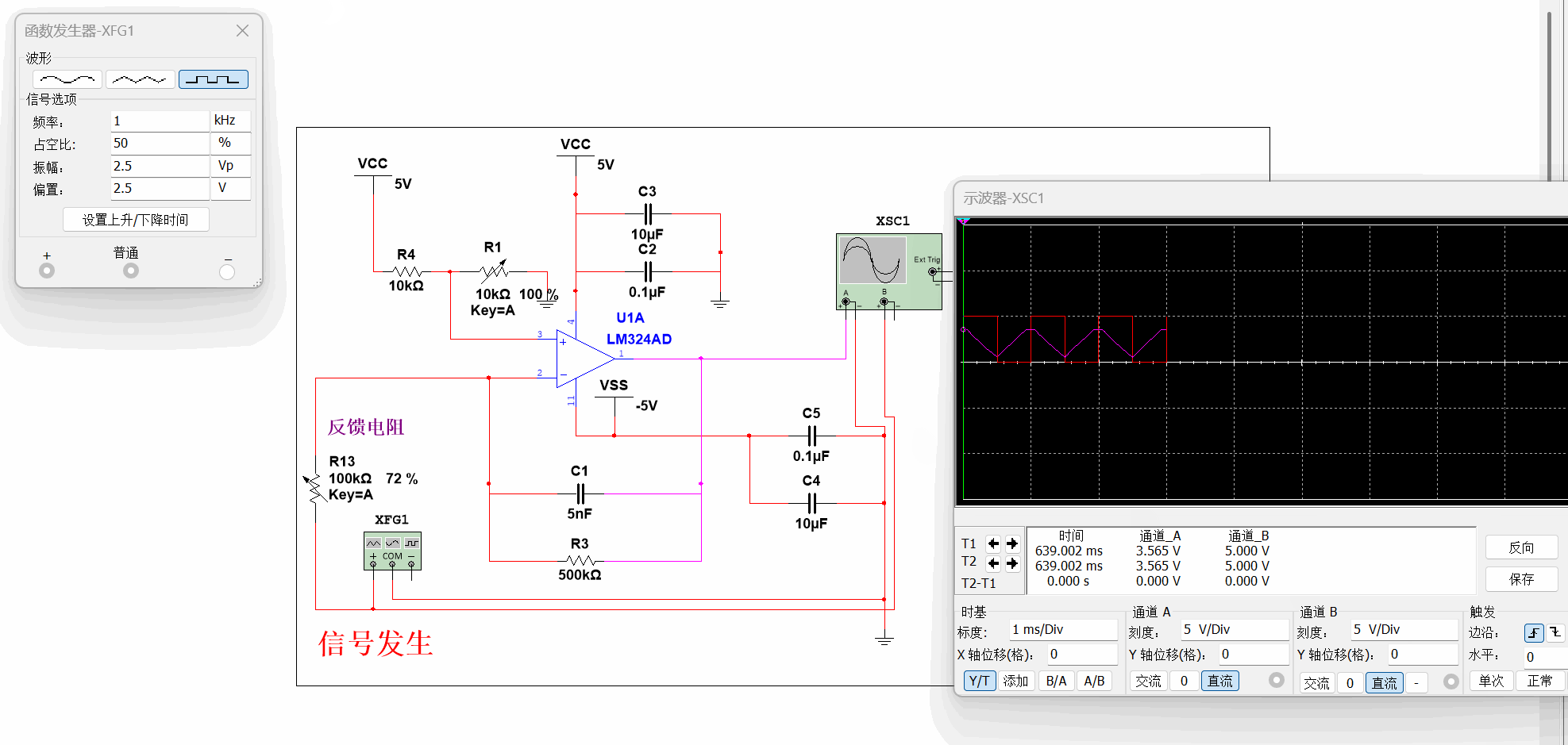
空口胡说显得有些纸上谈兵，直接上电路仿真~

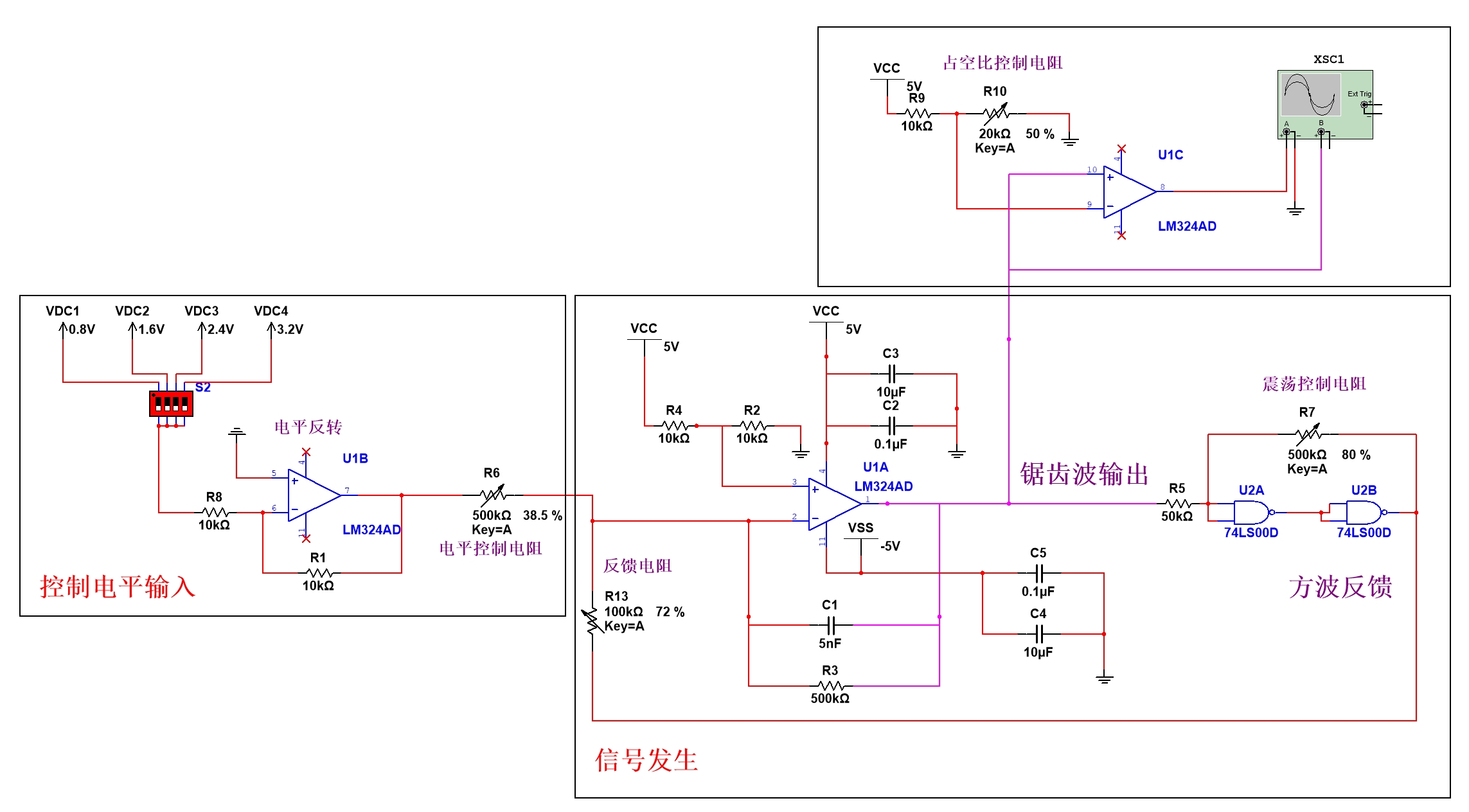
电路设计¶

仿真|可以戳这里访问百度网盘链接下载源文件

参数分析¶

关于电路原理就不再赘述了，相信原理图已经足够清晰

下面是主要参数的说明介绍，也建议按顺序扭动你的滑动变阻器呦~

震荡控制电阻R7反馈电阻R13电平控制电阻R6占空比电阻R10

这个电阻与其他电阻相关性较小，用于控制信号固有震荡频率
可大一些，不能太小

具体来说，有

\[ V_{T+}=V_T\left(1+\frac{R_5}{R_7}\right) \]

\[ V_{T-}=V_T\left(1-\frac{R_5}{R_7}\right) \]

即R7越大结果门限差越小，频率越高

但受电气特性影响，这个值很难计算，主要靠实际调整

最终，你需要调整门限范围，使得固有震荡频率超过所需最大频率

积分电路的R，同样控制固有频率，与震荡控制电阻配合食用

但需要注意支路电流，几十微安级，略大于最大电平控制电流，RC时间与设定频率接近

建议仿真通过后固定阻值，若不能起振先调触发器的电阻

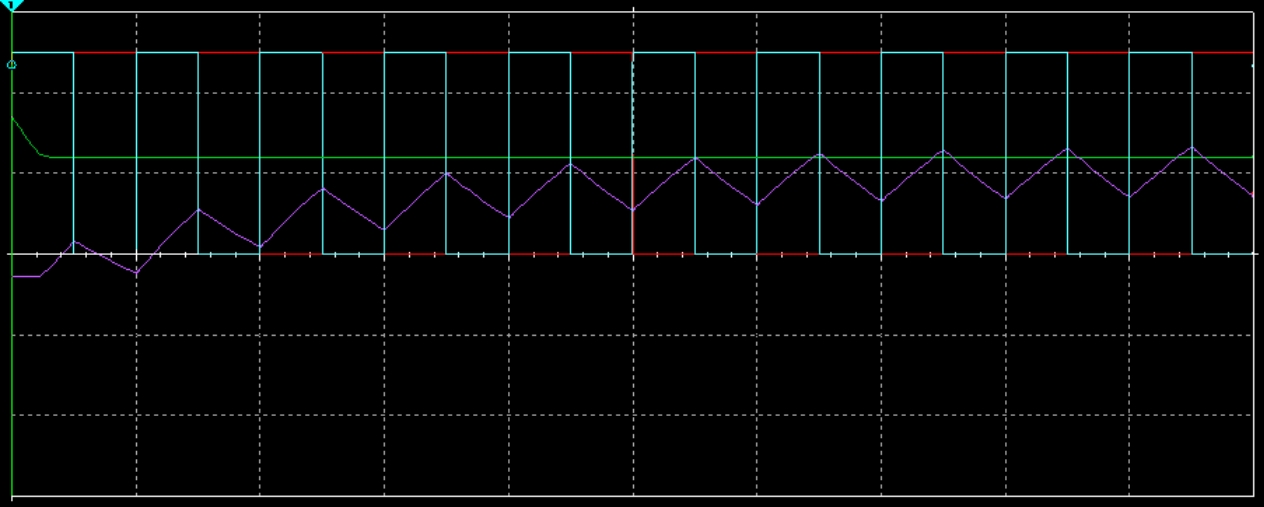
此时，在不接入电平的情况下，能产生5KHz左右的方波和三角波

这一电阻控制着四电平控制的频率步进（即电流）。随输入电平和反馈电阻变化而变化，故没有定值

没啥好算的，拿个500KHz滑动变阻器，从大阻值开始，直到步进满足要求即可🤪

到此，已经能生成四个频率符合要求的震荡信号啦

通过改变偏置电压门限来改变占空比

随便调🤌

仿真验证¶

最终仿真效果 | 频率、占空比可调

以上，算是为电赛划上了句号，无憾无悔