随机过程
只记录结论,详细见随机信号分析笔记
自相关函数
有定义式:
\[
R(t_1,t_2)=E[\xi(t_1)\xi(t_2)] = \int^{+\infty}_{-\infty}\int^{+\infty}_{-\infty}x_1x_2f(x_1,x_2;t_1,t_2)dx_2x_1
\]
令\(\tau=t_2-t_1\),有
\[
R(t_{1},t_{2})=R(t_{1},t_{1}+\tau)
\]
自相关函数的性质
自相关函数的作用
- 判断广义平稳
- 计算功率谱密度
- 求解平均、直流、交流功率
- 确定均值、方差
- 获得带宽信息
另有互相关系数
\[
R_{\xi\eta}(t_{1},t_{2})=E[\xi(t_{1})\eta(t_{2})]
\]
平稳随机过程
后讨论的随机过程均为广义平稳
各态历经性
任一样本经历了平稳过程的所有可能状态
作用
基于各态历经性(遍历性)用 【时间平均值】 代替 【统计平均值】 ,以减少计算量
时间平均值下的均值与自相关函数为
\[
\begin{array}{l}{\overline{{a}}=\overline{{x(t)}}=\displaystyle\operatorname*{lim}_{T\rightarrow\infty}\frac{1}{T}\int_{-T/2}^{T/2}x(t)d t}\\ {\overline{{R(\tau)}}=\displaystyle\operatorname*{lim}_{T\rightarrow\infty}\frac{1}{T}\int_{-T/2}^{T/2}x(t)x(t+\tau)d t}\end{array}
\]
即得到
\[
\begin{aligned}{a}&={\overline{{a}}}\\ {R\left(\tau\right)}&={R\left(\tau\right)}\end{aligned}
\]
功率谱密度 PSD
为了描述随机过程 X 的平均功率在各个频率上的分布情况,即【单位频带上的平均功率】
\[
P_{x}(f)=\operatorname*{lim}_{T\rightarrow\infty}\frac{\left|X_{T}(f)\right|^{2}}{T}
\]
\(X_{T}(f)\) 为样本函数\(x(t)\)的 截短函数 对应的 频谱函数X(jw)(1)
- 回忆 S&S 功率函数
\[
P_{\xi}(f)=E\left[P_{x}(f)\right]=\operatorname*{lim}_{T\rightarrow\infty}\frac{E\left|X_{T}(f)\right|^{2}}{T}
\]
表示对所有样本功率谱的统计平均值
基于自相关函数求解 PSD
有 FT 对 \(R(\tau)\Leftrightarrow P_{\xi}(\omega)\)
即维纳-辛钦定理
用角频率\(\omega\)表示
\[
\begin{aligned}&P_\xi(\omega)=\int_{-\infty}^\infty R(\tau)e^{-j\omega\tau}d\tau\\&R(\tau)=\frac{1}{2\pi}\int_{-\infty}^{\infty}P_{\xi}(\omega)e^{j\omega\tau}d\omega\end{aligned}
\]
这里的\(P_\xi(\omega)=G_X(\omega)\)
用频率\(f\)表示
\[
\begin{aligned}P_\xi(f)&=\int_{-\infty}^\infty R(\tau)e^{-j2\pi f\tau}d\tau\\R(\tau)&=\int_{-\infty}^\infty P_\xi(f)e^{j2\pi f\tau}df\end{aligned}
\]
典型变换
\[
\begin{aligned}&1\Leftrightarrow2\pi\delta(\omega)\\&\cos(\omega_0\tau)\Leftrightarrow\pi[\delta(\omega-\omega_0)+\delta(\omega+\omega_0)]\\&\sin(\omega_0\tau)\Leftrightarrow j\pi[\delta(\omega+\omega_0)-\delta(\omega-\omega_0)]\end{aligned}
\]
PSD 的性质
- 遍历过程任一样本的 PSD \(=\) 过程的 PSD
- 非负性
- 与 自相关函数 R 一样,为偶函数
作用
- 描述随机过程频域特性
- 积分计算带宽和平均功率
- 描述滤波器或其他器件对信号与噪声的影响
高斯随机过程
特性
- 从定义出发,若广义平稳,则一定狭义平稳
- 互不相关则独立统计
- 线性可加
一维概率密度函数
\[
f(x)={\frac{1}{\sqrt{2\pi}\sigma}}\exp\left(-{\frac{(x-a)^{2}}{2\sigma^{2}}}\right)
\]
一维分布函数 CDF
\[
F(b)=P(x\leq b)=\int_{-\infty}^{b}{\frac{1}{{\sqrt{2\pi}}\sigma}}\exp\left[-{\frac{(x-a)^{2}}{2\sigma^{2}}}\right]d x
\]
这并不好算,因此曲线救国
误差函数 | 补误差函数
已知
误差函数:\(e r f(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^{2}}d t\)
补误差函数:\(e r f c(x)=\frac{2}{\sqrt{\pi}}\int_{x}^{\infty}e^{-t^{2}}d t\)
基于指数积分—概率论笔记,容易得到
\[
\begin{array}{l}{{e r f(0)=0}}\\ {{e r f(\infty)=1}}\end{array}
\]
\[
\begin{aligned}&erf(-x)=-erf(x)\\&erfc(-x)=2-erfc(x)\end{aligned}
\]
\[
erfc(x)=1-erf(x)
\]
最终得到
\[
F(x)=\begin{cases}\frac{1}{2}+\frac{1}{2}erf\left(\frac{x-a}{\sqrt{2}\sigma}\right),&x\geq a\\\\1-\frac{1}{2}erfc\left(\frac{x-a}{\sqrt{2}\sigma}\right),&x<a&&\end{cases}
\]
推导过程
考虑 \(x\geq a\) ,有
\[
F(x)=\int_{-\infty}^{x}{\frac{1}{\sigma{\sqrt{2\pi}}}}\exp\left(-{\frac{(t-a)^{2}}{2\sigma^{2}}}\right)d t
\]
将积分中的变量 t 进行标准化。令:
\[
z={\frac{t-a}{\sigma{\sqrt{2}}}}
\]
则有:
\[
d t=\sigma{\sqrt{2}}\,d z
\]
修正上下限,分布函数为
\[
F(x)=\int_{-\infty}^{\frac{x-a}{\sigma\sqrt{2}}}\frac{1}{\sqrt{\pi}}e^{-z^{2}}d z
\]
与误差函数对比,结合分布函数正向趋向于 1,可得
\[
F(x)=\frac{1}{2}+\frac{1}{2}erf\left(\frac{x-a}{\sqrt{2}\sigma}\right)
\]
反之用补误差函数表示
平稳随机过程通过线性系统
随手记
\[
\begin{array}{l}{F(\mathrm{j}0)=\displaystyle\int_{-\infty}^{+\infty}f(t)\mathrm{d}t}\\ {f(0)=\displaystyle\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\mathrm{j}\omega)\mathrm{d}\omega}\end{array}
\]
- \(H(0)=\int_{0}^{\infty}h(t)d t\) 是线性系统的直流增益; \(\left|H(f)\right|^{2}\) 是功率增益
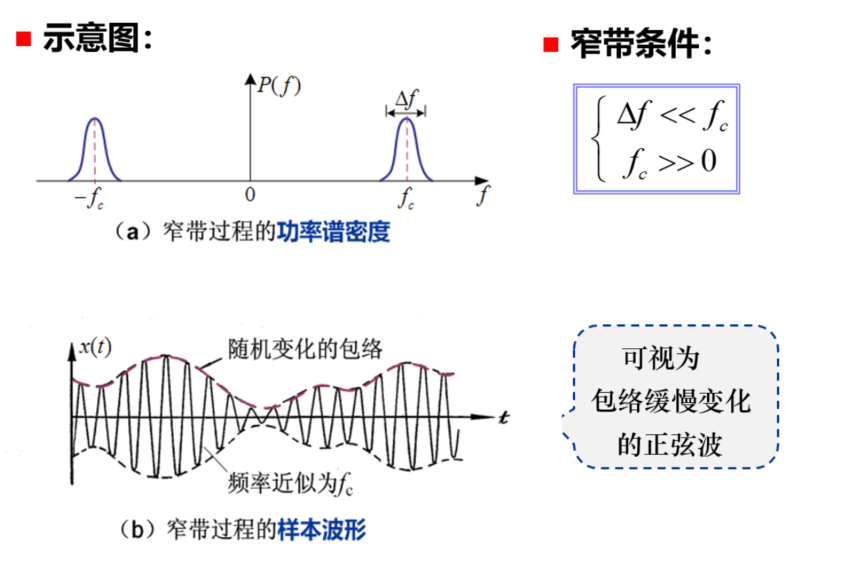
窄带随机过程
为窄带高斯噪声铺垫
满足条件:功率谱密度下 谱密度集中在中心频率附近,且中心频率远离零频
表达形式
这一小节十分滴重要,解调中求制度增益 | 数字调制的误码率都会用到
\[
\xi(t)=a_{\xi}(t)\cos[\omega_{c}t+\varphi_{\xi}(t)],\quad a_{\xi}(t)\geq0
\]
\[
a_\xi(t)\text{为随机包络,}\varphi_\xi(t)\text{为随机相位}
\]
随机包络、随机相位的统计特性
因 \(\xi_{c}(t)\) \(\xi_{s}(t)\) 互不相关,可用直接相乘计算联合密度函数,再分别计算边缘密度函数,得
统计独立: \(f(a_{\xi},\varphi_{\xi})=f(a_{\xi})\cdot f(\varphi_{\xi})\)
随机包络为【瑞利分布】: \(f(a_{\xi})=\frac{a_{\xi}}{\sigma_{\xi}^{2}}\exp\left[-\frac{a_{\xi}^{2}}{2\sigma_{\xi}^{2}}\right]\left(a_{\xi}\geq0\right)\)
随机相位为【均匀分布】:f(φξ ) = \(f(\varphi_{\xi})=\frac{1}{2\pi}\quad(0\leq\varphi_{\xi}\leq2\pi)\)
\[
\xi(t)=\xi_{c}(t)\cos\omega_{c}t-\xi_{s}(t)\sin\omega_{c}t
\]
\[
a_\xi(t)\text{同向分量,}\varphi_\xi(t)\text{为正交分量}
\]
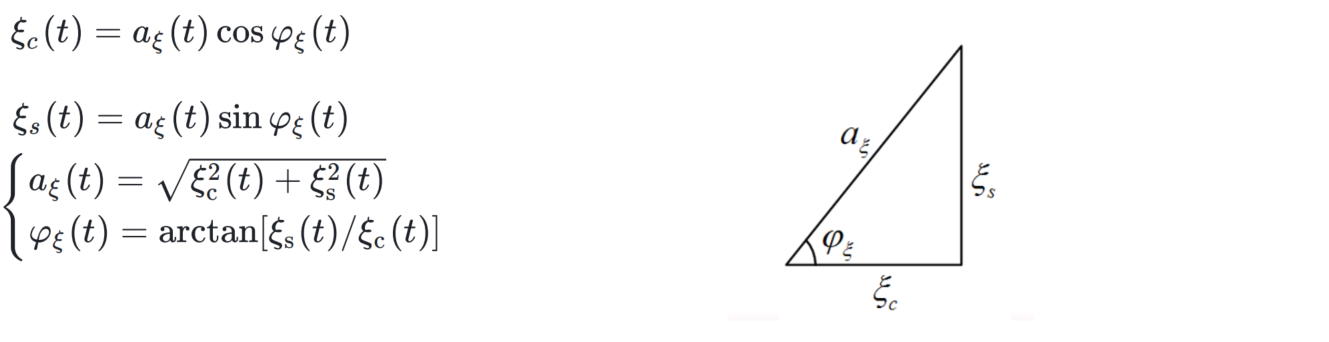
同向、正交分量的统计特性
均值 0、方差 \(\sigma_{\xi}^{2}\) 的平稳高斯窄带过程 ,它的同向 | 正交分量同样也是平稳高斯过程
且均值,方差相等,即 \(\sigma_{\xi}^{2}=\sigma_{c}^{2}=\sigma_{s}^{2}\)
并且同向分量与正交分量的互相关函数 \(R_{c s}(0)=R_{s c}(0)=0\rightarrow\) 同一时刻互不相关
二者关系
正弦波 + 窄带高斯过程
常见的前级输入未处理信号
有合成信号
\[
\begin{aligned}r(t)=A\cos(\omega_ct+\theta)+n(t)&=A\cos(\omega_ct+\theta)+n_c(t)\cos\omega_ct-n_s(t)\sin\omega_ct\\&=z_c(t)\cos\omega_ct-z_s(t)\sin\omega_ct\\&=z(t)\cos[\omega_ct+\varphi(t)]\end{aligned}
\]
联合上一节思路求解 | 包络 | 相位 | 统计特征
\[
\xrightarrow{\text{统计独立}}f(z_{\mathfrak{c}},z_{\mathfrak{s}}/\theta)\xrightarrow{|J|}f(z,\varphi/\theta)\xrightarrow{\text{边际分布}}
\]
得 \(z(t)\sim\) 广义瑞利分布, 又称莱斯 \((R i c e)\) 分布:
\[
f(z)=\frac{z}{\sigma^{2}}\exp\left[-\frac{1}{2\sigma^{2}}(z^{2}+A^{2})\right]I_{0}\left(\frac{A z}{\sigma^{2}}\right),z\ge0
\]
\(I_{0}(x)\) 是零阶修正贝塞尔函数;当 \(x\geq0\) 时, \({I}_{0}(x)\) 单调上升,且 \(I_{0}(0)=1\)
- 当 \(\mathsf{A}\to\mathsf{0}\) 时, \(\mathsf{f}\left(z\right)\) 退化为 瑞利分布(只有噪声)
- 当 SNR 比较大时, \(\mathsf{f}\left(z\right)\) 近似为 高斯分布
- 相位密度函数不再服从均匀分布
常见信号
\[
V(t)=\sqrt{[a+n_{c}(t)]^{2}+n_{s}^{2}(t)}
\]
\[
V(t)=\sqrt{n_{c}^{2}(t)+n_{s}^{2}(t)}
\]
\[
\frac{A\cos(\omega_ct+\theta)}{\begin{array}{c}\text{信号功率}\\A^2/2\end{array}}+\frac{n(t)}{\begin{array}{c}\text{噪声功率}\\\sigma^2_{\xi}\end{array}}
\]
\(S N R=\frac{A^{2}}{2\sigma_{\xi}^{2}}\)
为功率之比
高斯白噪声与带限白噪声
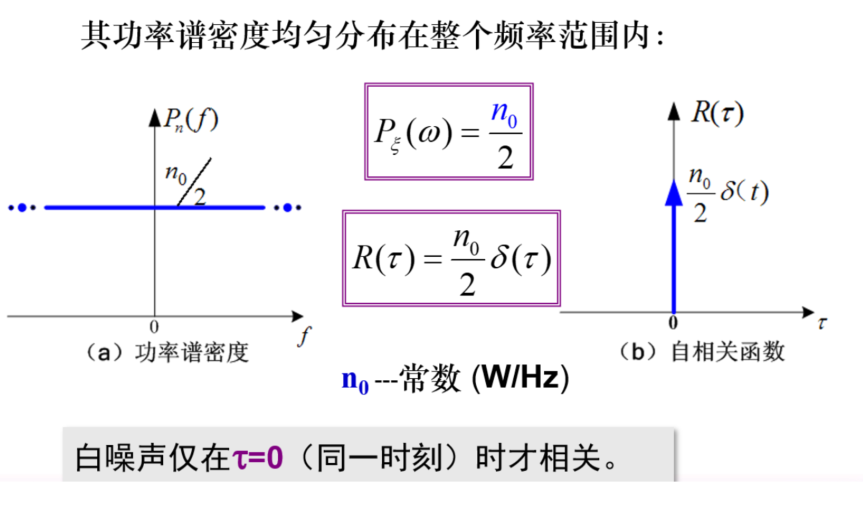
白噪声
- PSD 均匀分布(远远大于功率频带宽度)
- 时域上自相关函数为只在 0 的冲激函数
- 平均功率无穷大
白噪声仅在 \(\tau{=}0\) (同一时刻)时才相关
高斯白噪声
指概率分布服从高斯分布的白噪声
高斯白噪声在任意两个不同时刻上的取值之间,不仅是互不相关的,而且还是统计独立的
限带白噪声
- 低通白噪声
PSD : \(P_n(f)=\begin{cases}&\frac{n_0}{2},&|f|\leq f_H\\&0,\text{其他}&&\end{cases}\)
自相关函数: \(R(\tau)=n_{0}f_{H}\frac{\sin{2\pi f_{H}\tau}}{2\pi f_{H}\tau}\)
就是 频域矩形信号 与 时域采样信号 的 FT/IF
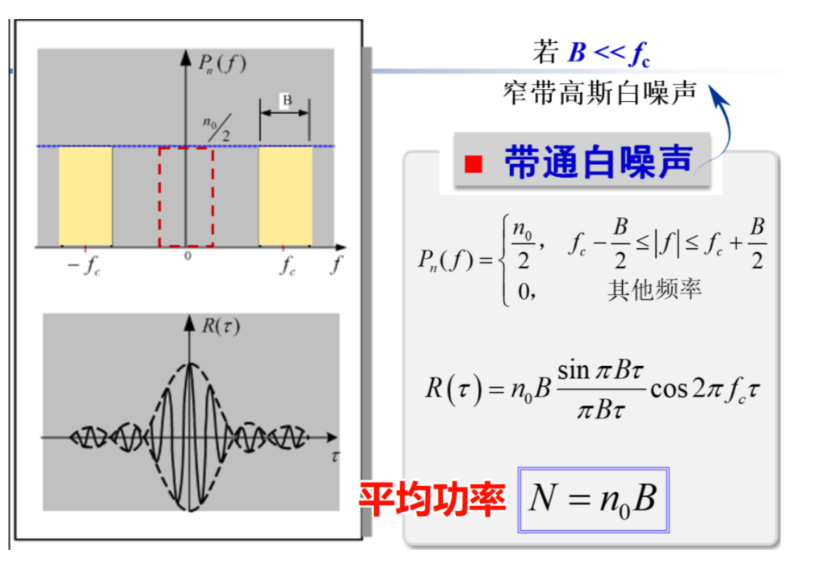
- 带通白噪声