信源编码
作用:压缩 | ADC
知识点
波形编码 | 抽样、量化、编码
模拟脉冲调制 PAM PDM PPM | PCM、DPCM、ΔM
时分复用【TDM】
抽样
题外话
在 w与f 的转化时,发现有些会乘 \(\frac{1}{2\pi}\) 有的却没有变换,只是把 w 变成 f
一般信号变换时,有两种
- 一般变换,遵守 FT 性质
如对冲击信号,有
\[
\begin{aligned}&{\displaystyle\delta(\omega-\omega_{\mathrm{c}})=\delta(2\pi f-2\pi f_{\mathrm{c}})=\frac{1}{2\pi}\delta(f-f_{\mathrm{c}})}\\ &{\displaystyle\delta(\omega+\omega_{\mathrm{c}})=\delta(2\pi f+2\pi f_{\mathrm{c}})=\frac{1}{2\pi}\delta(f+f_{\mathrm{c}})}\end{aligned}
\]
- 带移操作,对信号(函数)位移
即对于以 w 和 f 两种变量,有
\[
\begin{aligned}{{\displaystyle{\mathcal F}\{m(t)\cos(\omega_{c}t)\}=\frac{1}{2}\left[M(\omega-\omega_{c})+M(\omega+\omega_{c})\right]}}\\ {{\displaystyle{\mathcal F}\{m(t)\cos(\omega_{c}t)\}=\frac{1}{2}\left[M(\omega-\omega_{c})+M(\omega+\omega_{c})\right]}}\end{aligned}
\]
举个例子
将
\[
S_{\mathrm{AM}}(\omega)=\pi A_{0}\left[\delta(\omega+\omega_{c})+\delta(\omega-\omega_{c})\right]+\frac{1}{2}\left[M(\omega+\omega_{c})+M(\omega-\omega_{c})\right]
\]
转化为 f,有
\[
S_{\mathrm{AM}}(f)=\pi A_{0}\left[\frac{1}{2\pi}\delta(f+f_{\mathrm{c}})+\frac{1}{2\pi}\delta(f-f_{\mathrm{c}})\right]+\frac{1}{2}\left[M(f+f_{\mathrm{c}})+M(f-f_{\mathrm{c}})\right]\,.
\]
低通抽样
理想抽样信号 = 输入信号 · 周期序列冲激信号,即
\[
x_s(t)=x(t)p(t)
\]
其中
\[
p(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_s)
\]
对于理想 P(jw) 有
\[
P(\mathrm{j}\omega)\:=\:\frac{2\pi}{T_s}\sum_{k=-\infty}^{+\infty}\delta(\omega-n\omega_s)
\]
利用卷积的性质,则有
\[
x_{s}(t)=x(t)\bullet\sum_{n=-\infty}^{+\infty}\delta(t-nT_{s})=\sum_{n=-\infty}^{+\infty}x(nT_{s})\delta(t-nT_{s})
\]
另外,在 FT 变换域中表现为卷积,即
\[
X_s(\text{j}\omega)=\frac{1}{2\pi}X(\text{j}\omega)*P(\text{j}\omega)
\]
得
\[
X_{s}(j\omega)=\frac{1}{T_{s}}\sum_{n=-\infty}^{\infty}X(j(\omega-n\omega_{s}))
\]
由于信号 x(t) 只占一定的频率范围,可写为
\[
\begin{aligned}
X_{\mathrm{s}}\left(\mathrm{j}\omega\right)& =\frac{1}{2\pi}X(\mathrm{j}\omega)*P(\mathrm{j}\omega)=\frac{1}{T_{s}}X(\mathrm{j}\omega)*\sum_{n=-\infty}^{+\infty}\delta(\omega-n\omega_{s}) \\
&=\frac{1}{T_{s}}\sum_{n=-\infty}^{+\infty}X\left(\mathrm{j}(\omega-n\omega_{s})\right)\left[u\left(\omega-n\omega_{s}+\omega_{\mathrm{m}}\right)-u\left(\omega-n\omega_{s}-\omega_{\mathrm{m}}\right)\right]
\end{aligned}
\]
用频率 f 表示,有
\[
M_s(f)=\frac{1}{T_s}\sum_{n=-\infty}^\infty M(f-nf_s)=\frac{1}{T_s}M(f)+\frac{1}{T_s}\sum_{n\neq0}M(f-nf_s)
\]
其中,最低 抽样 频率为\(f_s=\frac{\omega_s}{2\pi}=\frac{\omega_\mathrm{m}}{\pi}=2f_\mathrm{m}\),\(f_m\)为 信号 最高频率
带通抽样
带通判定:信号最低频 fL \(>\) 带宽 B
抽样速率
实际带宽的两倍多一些
频谱的周期延拓是否会发生混叠
\[
f_{s}=2B(1+\frac{k}{n})
\]
\[
\text{式中,}B=f_H-f_L
\]
\[
n\text{为}(f_H/B)\text{的【整数部分】};k\text{为}(f_H/B)\text{ 的【小数部分,如 }0.5\mathrm{】}
\]
其中
!!! info ""

模拟脉冲调制之 PAM
PAM
- 脉冲幅度调制,即抽样的结果
- 实际上用一定宽度的矩形脉冲序列采样
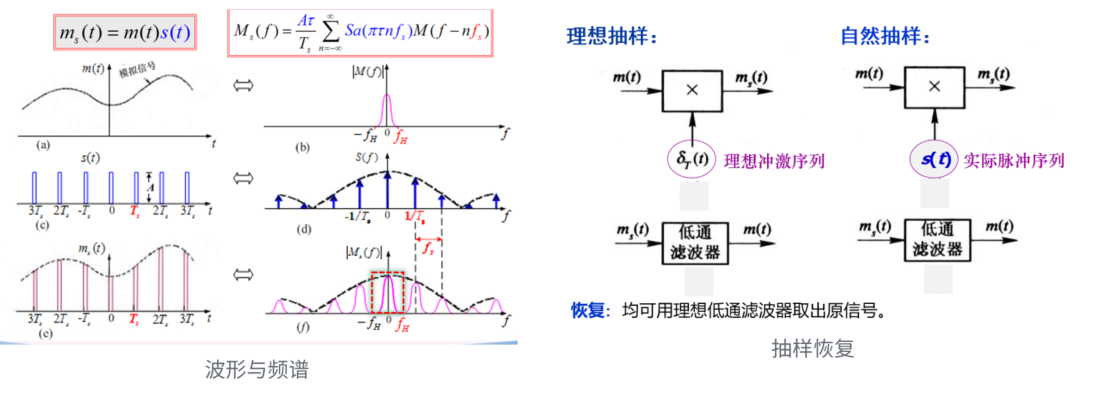
自然抽样过程
与理想抽样结果相比,多了矩形信号 FT 后的 Sa 信号
\[
M_{s}(f)=\frac{E\tau}{T_{s}}\sum_{n=-\infty}^{\infty}S a(\pi\tau n f_{s})M(f-n f_{s})
\]
相较于平顶抽样,顶部随模拟信号变化
满足采样定理即可用 LPF 恢复信号
平顶抽样过程
抽样 + 保持
时域上为采样信号与保持信号 \({h}({t})\) 卷积,即最后有
\[
M_{\mathrm{H}}(f)={\frac{1}{T_{s}}}H(f)\sum_{n=-\infty}^{\infty}M(f-n f_{s})
\]
对于信号恢复,也需要先通过【修正滤波器】 \(\frac{1}{H(f)}\) ,即
\[
\begin{array}{l}{\displaystyle M_{\mathrm{H}}(f)=\frac{1}{T_{s}}\sum_{n=-\infty}^{\infty}H(f)M(f-n f_{s})}\\ {\displaystyle=\frac{1}{T_{s}}H(f)M(f)+\frac{1}{T_{s}}\sum_{n\neq0}H(f)M(f-n f_{s})}\end{array}
\]
针对 n=0
\[
\hat{M}(f)=M_{\mathrm{H}}(f)\frac{1}{H(f)}H_{\mathrm{L}}(f)=\frac{1}{T_{s}}M(f)
\]
量化编码
概念定义
- 分层电平 \(m_{i}\)
- 量化间隔 \(\Delta v_{i}\)
- 量化电平\(q_{i}\),为间隔中点
\[
m_{q}(k T_{s})=q_{i}\qquad m_{i-1}\leq m(k T_{s})\leq m_{i}
\]
- 将抽样值表示为 \(m_{k}\) ,量化值为 \(m_{q}\)
- 均匀量化
\[
\Delta\nu=\frac{b-a}{M}\ [\mathsf{a},\mathsf{b}]
\]
主要应用于均匀分布大信号
\[
e_{q}=|m_{k}-m_{q}|
\]
量化噪声功率 \(N_{q}\) 为量化噪声的均方值
\[
\boxed{N_{\mathrm{q}}=E\Big[(m_{k}-m_{\mathrm{q}})^{2}\Big]=\int_{a}^{b}(x-m_{\mathrm{q}})^{2}f(x)\mathrm{d}x}
\]
抽样值平均功率 S
\[
\boxed{S=E\left[(m_{k})^{2}\right]=\int_{a}^{b}x^{2}f(x)d x}
\]
得信号量噪比表达式
\[
\boxed{\frac{S}{N_q}=\frac{E\left[m_k^2\right]}{E\left[\left(m_k-m_q\right)^2\right]}}
\]
例

即\(M^2\) or \(6N\) ,N 为所占编码位数
均匀量化的缺点
- 小信号下受限于最小分辨率,M 较小,S/Nq 小
- 需要编码位数大,占用带宽
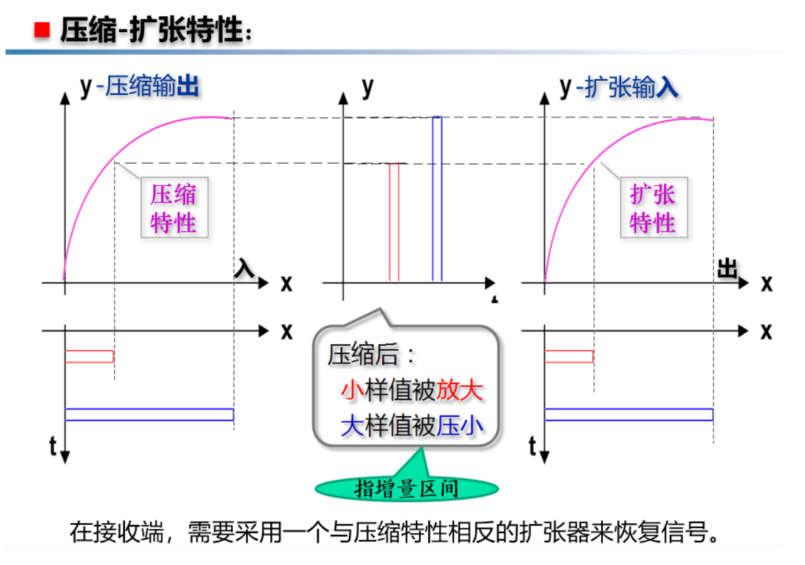
非均匀量化
采用对数压缩 + 均匀量化
A 压缩律 13 折线近似法
\[
y=\begin{cases}\frac{Ax}{1+\ln A},&0<x\leq\frac{1}{A}\\\frac{1+\ln Ax}{1+\ln A},&\frac{1}{A}\leq x\leq1&\end{cases}
\]
然而非线性电路上不易实现,故用折线近似
取经验值87.6,使得第一段斜率为 16,共八段,满足 2 的幂次
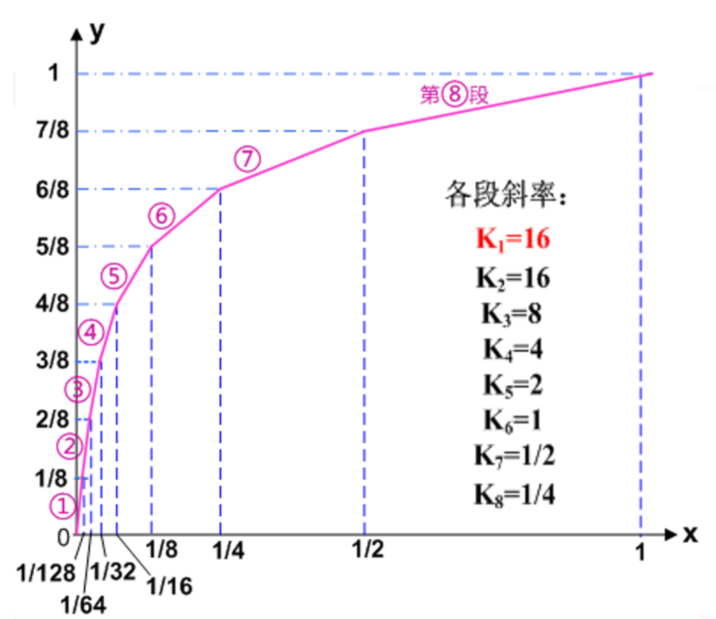
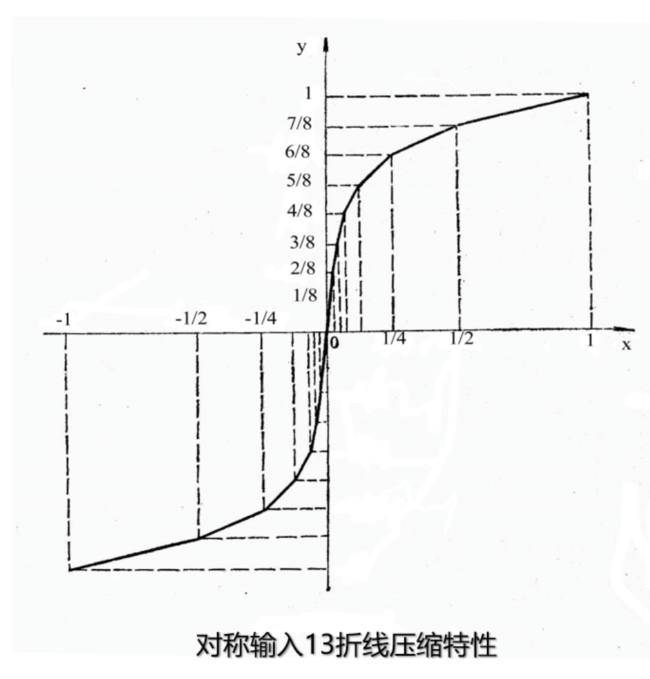
加上负极性的 8 段,结合靠近原点两段斜率相等,共 \(8\!+\!8\!-\!4\!+\!1\!=\!13\) 段,故称之 13 折线
脉冲编码调制—PCM
PCM 与 PAM 的关联
发送端
\[
\text{模拟信号}\to\boxed{\text{抽样保持}}\to\text{时间离散}PAM\text{信号}\to\boxed{\text{量化编码}}\to PCM\text{二进制信号}
\]
接收端
\[
PCM\text{信号}\to\boxed{\text{译码}}\to\text{时间离散}PAM\text{信号}\to\boxed{LPF}\to\text{模拟信号}
\]
基于 A 律十三折线的 PCM 编码
以四位为例,注意感受对称
正负极性
| 序号
| 折叠二进制码
|
正极性
| 15
| 1111
|
14
| 1110
|
...
| ...
|
8
| 1000
|
负极性
| 7
| 0000
|
...
| ....
|
1
| 0110
|
0
| 0111
|
16 段折线,每一段量化为 16 份,故需要 256 个,即 8 位
编号分别规定为【极性码】 【段落码】 【段内码】
基于 A 律
量化单位
\(\Delta={\frac{1}{128}}*{\frac{1}{16}}={\frac{1}{2048}}\) (看一半[0~a])
1/128 指的是横坐标(这里的最大值为 1),1/16 指的是一段分为 16 份
量化间隔
x 轴每一段的电平差(范围)/16
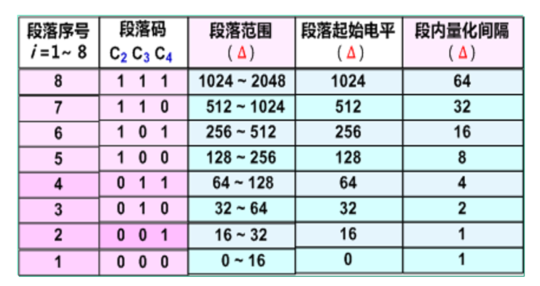
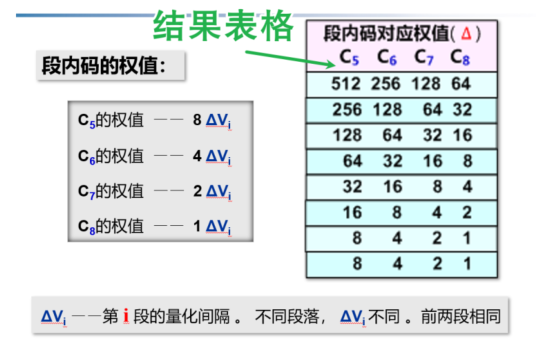
如此,能得到 \(\Delta\) 为单位的段落码、段内码与起始电平情况
- 量化间隔从 1 开始,为{1 1 2 4 8 16 32 64}
- 起始电平分别为{0 16 32 64 128 256 512 1024},确定段落码
- 段落确定量化间隔,确定权值 \(\rightarrow\) 段内码
!!! info ""
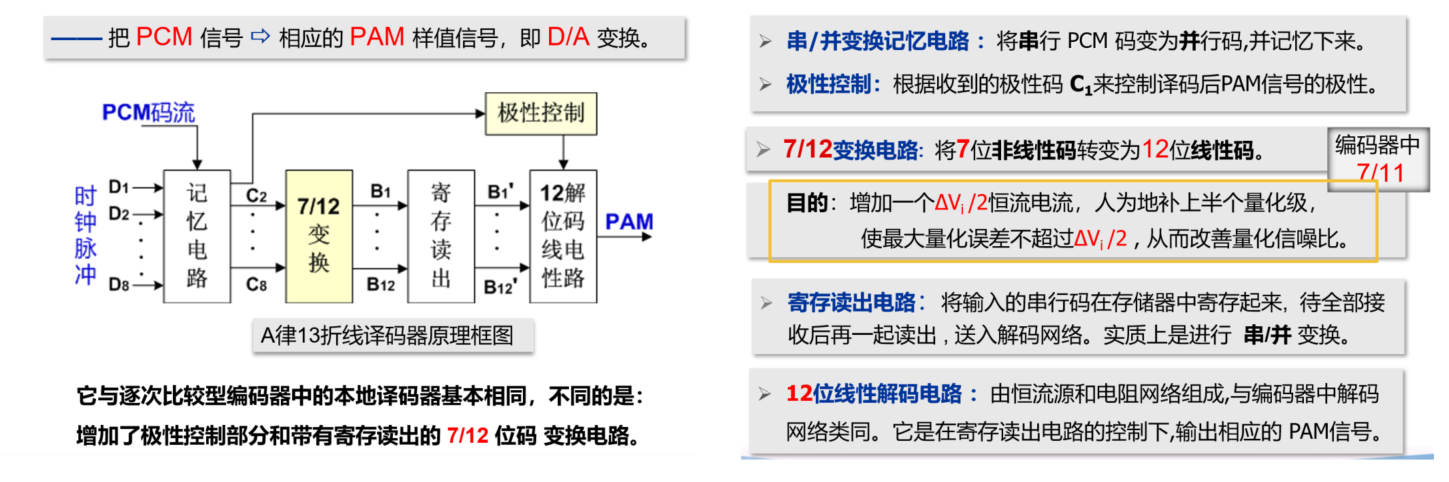
编译码器
类比数电最后一章
编码
例

译码
!!! example "例"
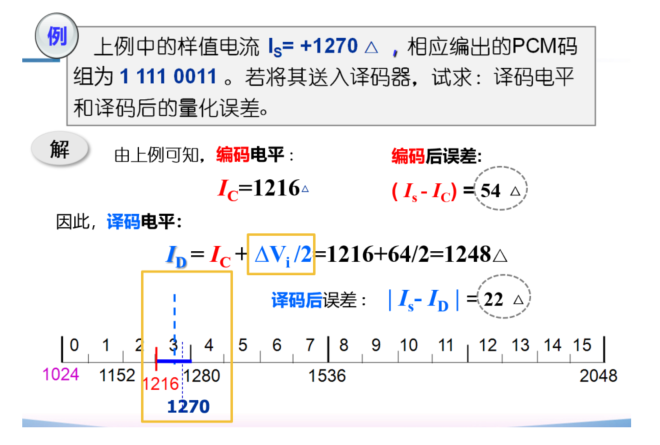
例
\(若4律13折成编码路的过载电平是5V,即编码范围[-5V,+5V]\\输入抽样脉冲幅度是-0.95V\\1. 求编码器输出码组,并计算量化误差\\2. 写出该7位码所对应的11位线性码\\3. 计算译码器输出的量化电平\)
注意归一化
\(\Delta=5\cdot\frac{1}{2048}\)
答案:
- \(0\text{ 101 1000 ; 误差:5 }\Delta=0.012V\)
- \(\text{0011000000}\)
- \(-392\Delta=-0.957V\)
区别【编码电平】【均匀量化码】【译码电平】
- 编码是身份证号,有对应的规则,有单位
- 均匀量化码是编码电平值的二进制表达(7 位 →11 位,因为编码最大为 2048)
- 译码电平是编码电平 + 一半量化间隔,是译码器的输出
7-12 位中最低位从 \(2^{-1}\) 开始
PCM 比特率与带宽
比特率计算公式 | N 为二进制编码位数
\[
R_{b}=f_{s}\cdot N=2f_{H}\cdot N
\]
传输带宽计算公式(非归零矩形脉冲传输)(占空比 =1 )
\[
B=R_{s}=R_{b}=f_{s}\cdot N
\]
PCM 最小带宽 \(B=N\cdot f_{H}\) ,规避码间串扰
故\(R_b\)不得超过 \(2B\),本质上是受限于采样定理
输出噪声与指标
输出信号 = 信号成分 + 量化噪声 + 加性噪声(热噪声)
指标
- 抗加性噪声性能 \(\frac{S_{o}}{N_{\mathrm{a}}}=\frac{E[m^{2}(t)]}{E[n_{\mathrm{a}}^{2}(t)]}\)
- 抗量化噪声性能 \(\frac{S_{o}}{N_{q}}=\frac{E[m^{2}(t)]}{E[n_{q}^{2}(t)]}\)
- 总输出 SNR \(\frac{S_{o}}{N_{o}}=\frac{E[m^{2}(t)]}{E[n_{q}^{2}(t)]+E[n_{o}^{2}(t)]}\)
当存在自然码编码、均匀量化、输入信号均匀分布前置条件时
【抗加性噪声性能】
\[
\frac{S_{o}}{N_{\mathrm{a}}}=\frac{E[m^{2}(t)]}{E[n_{\mathrm{a}}^{2}(t)]}=M^{2}\mathrm{~/~}2^{2(N+1)}\;P_{e}=\frac{1}{4P_{e}}
\]
\(P_{e}\) 为误码率
【抗量化噪声性能】
\[
{\frac{S_{0}}{N_{q}}}={\frac{E[m^{2}(t)]}{E[n_{q}^{2}(t)]}}=M^{2}=2^{2\color{red}N}=2^{2\color{red}{B/f_{\mathrm{H}}}}
\]
\[
{\frac{S_{0}}{N_{q}}}(d B)=20\log M
\]
【总输出】
\[
\frac{S_{\mathrm{o}}}{N_{\mathrm{o}}}=\frac{E[m^{2}(t)]}{E[n_{\mathrm{a}}^{2}(t)]+E[n_{\mathrm{q}}^{2}(t)]}=\frac{S_{\mathrm{o}}/N_{q}}{1+N_{\mathrm{a}}/N_{\mathrm{q}}}=\frac{2^{2N}}{1+4P_{\mathrm{e}}2^{2N}}
\]
差分脉冲编码调制 DPCM
利用相邻抽样值之间的相关性,降低编码信号比特率,压缩信号带宽
方法之一为预测编码
预测编码
基于上一个值预测现值,并对实际预测误差进行编码
利用差值较小 | 编码译码预测算法一致的特性
使能够只传输差值(抓取小数值特征值传输)来通信
了解一下
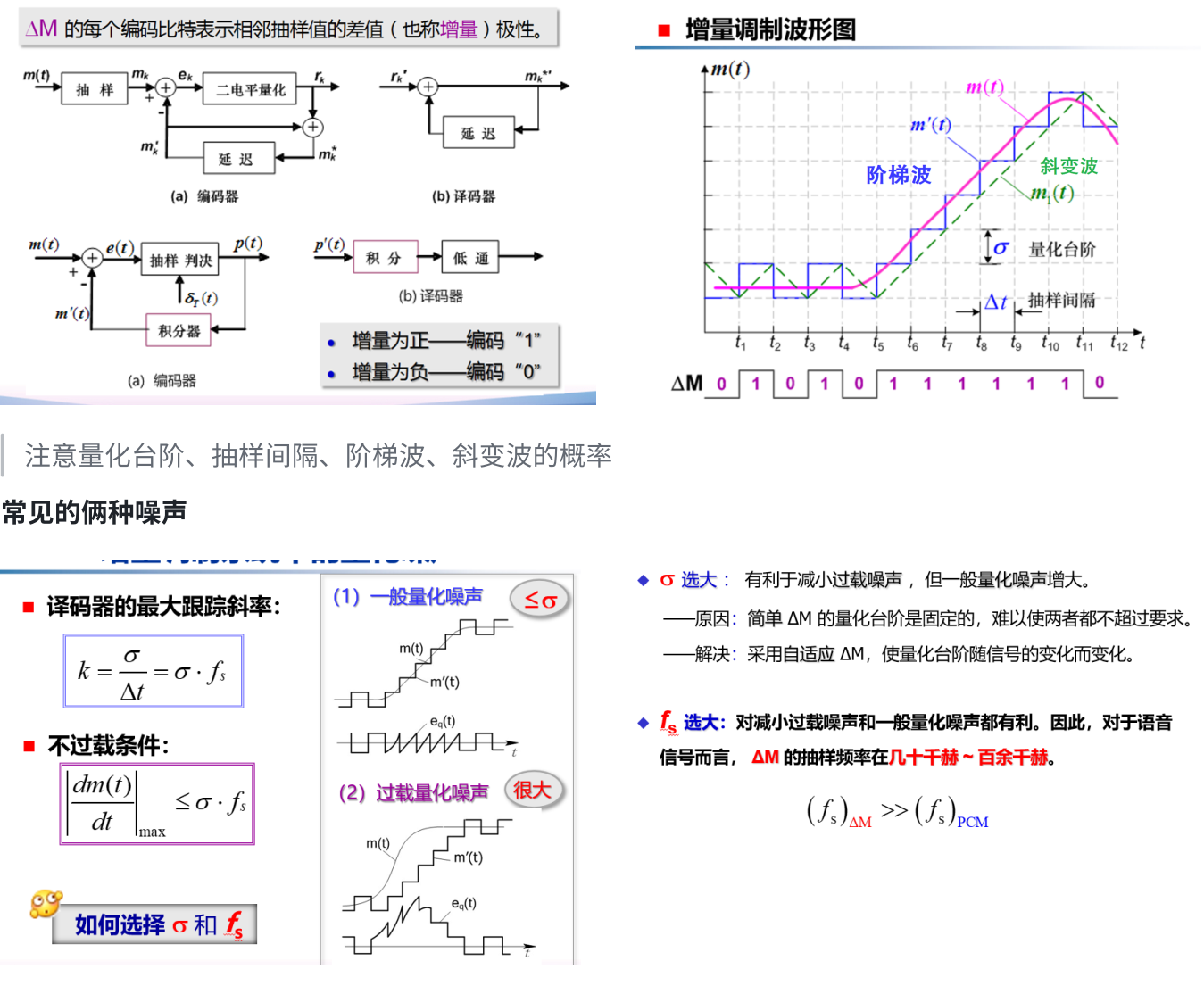
增量调制 ΔM
与 PCM 相比,编译码简单,低比特率时的量化信噪比高,抗误码特性好等优点
广泛用在军事和工业部门的专用通信网和卫星通信中
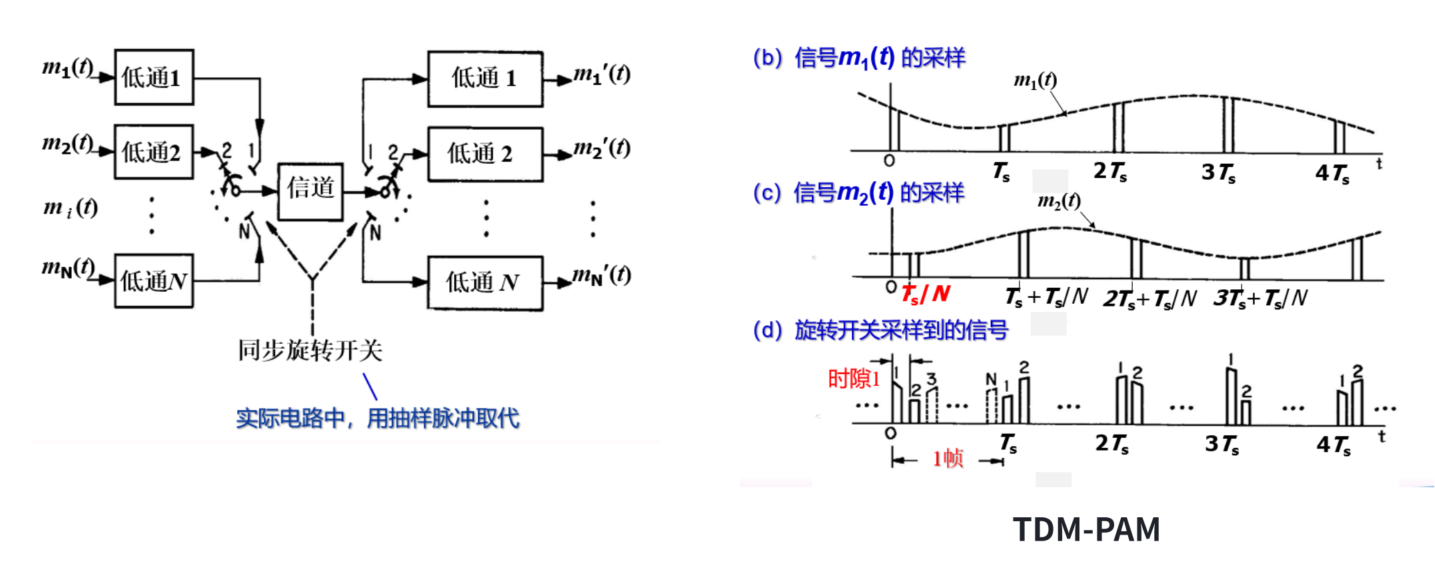
时分复用 TDM
类比计网时分复用传输
注意信道选通同步