跳转至

信道

 

约 1368 个字 预计阅读时间 8 分钟

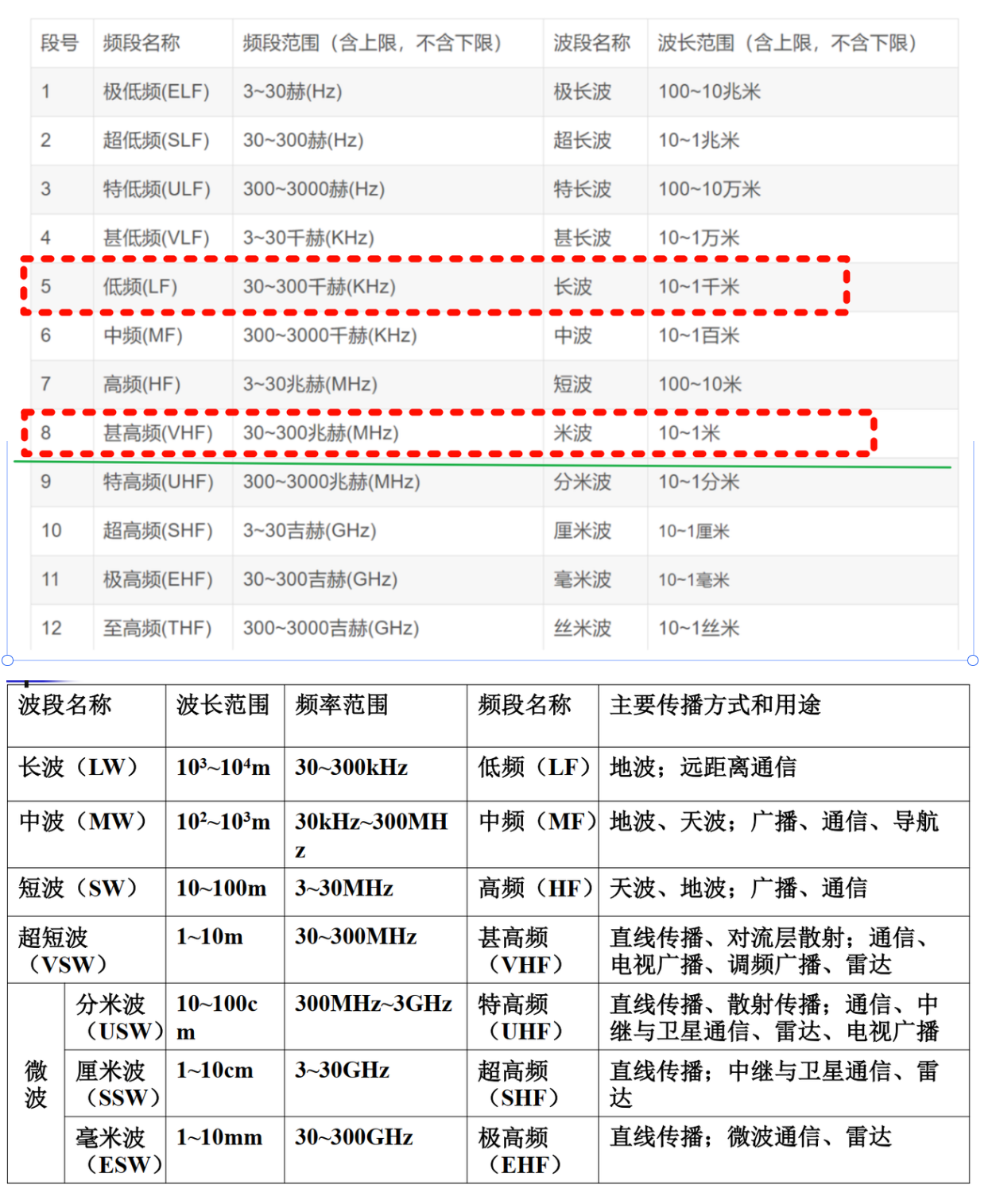
常见无线波段与应用

信道分类

  1. 狭义信道
  • 有线信道
  • 无线信道
  1. 广义信道
  • 调制信道（关注调制/解调问题）
  • 编码信道（关注编码/译码问题）

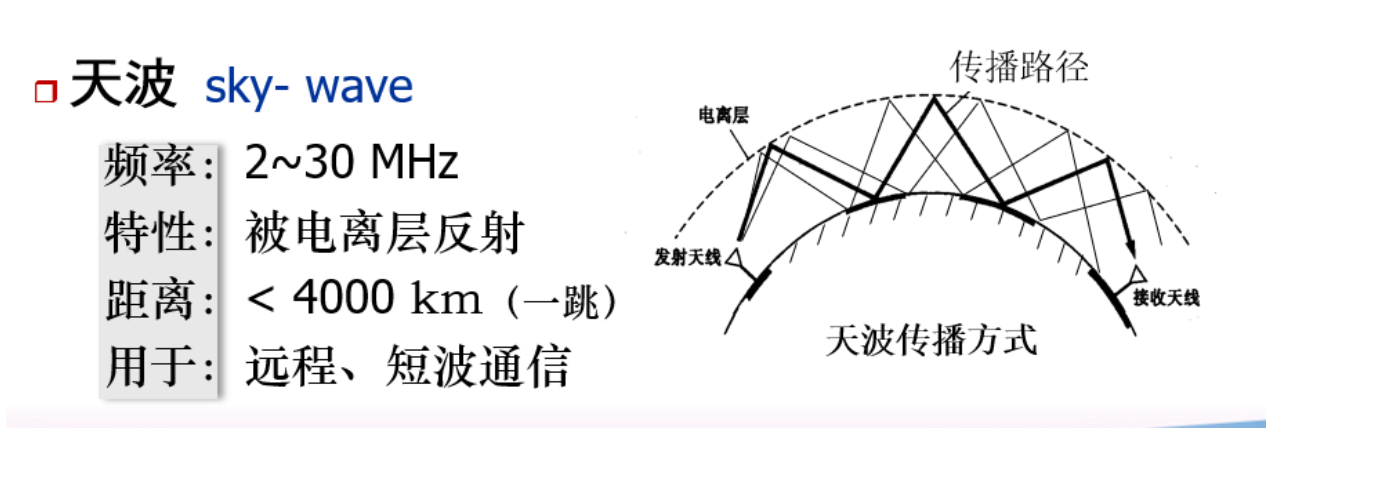
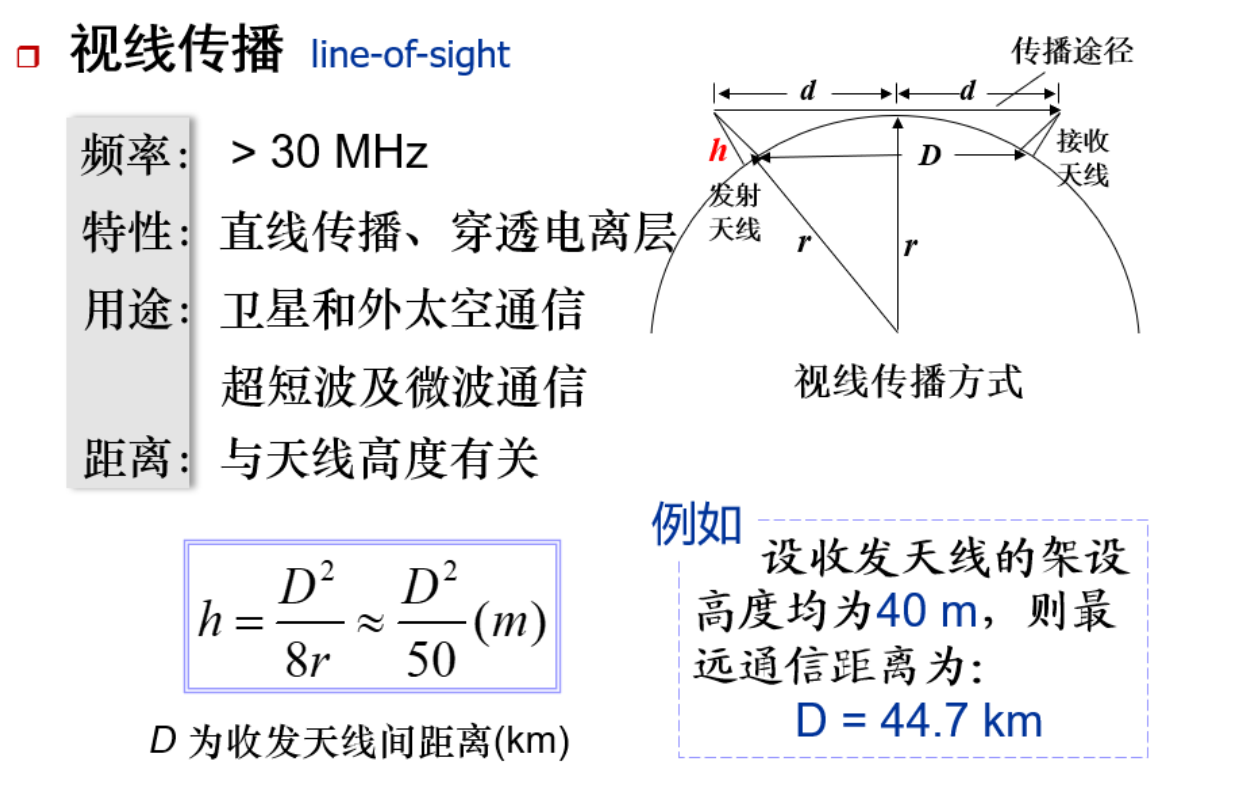
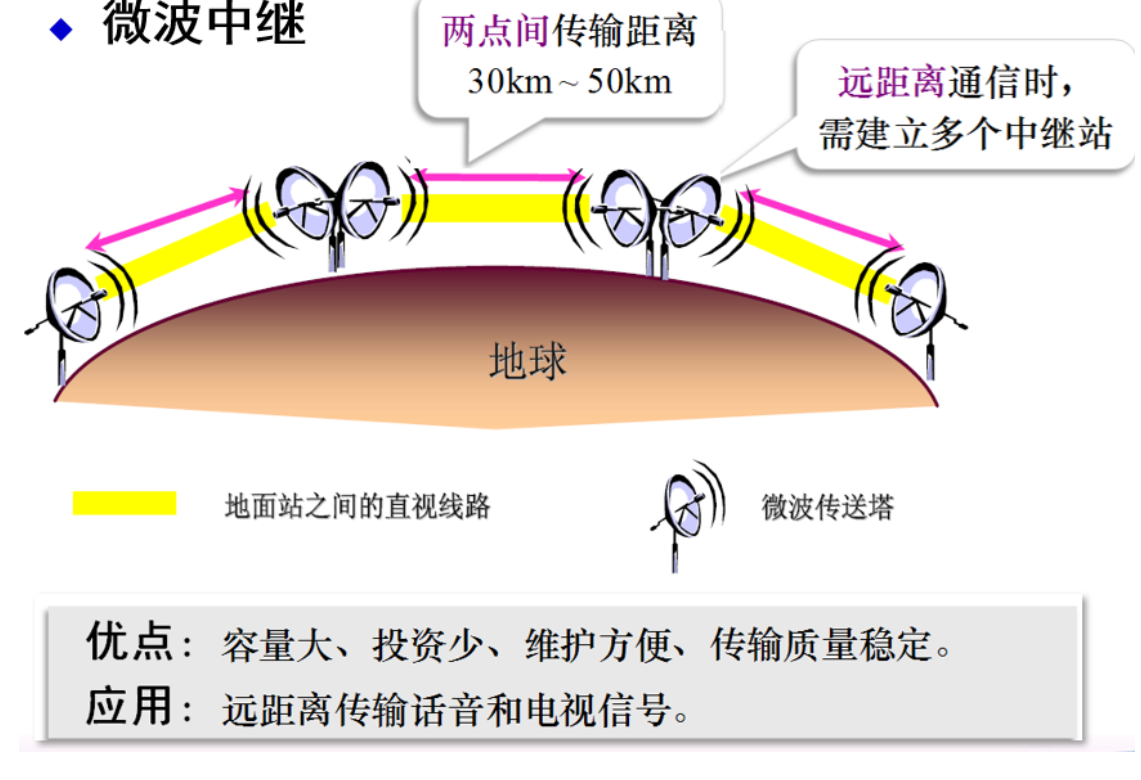
无线信道传播方式

地波

天波

视距点对点传输

即 RF 射频范畴

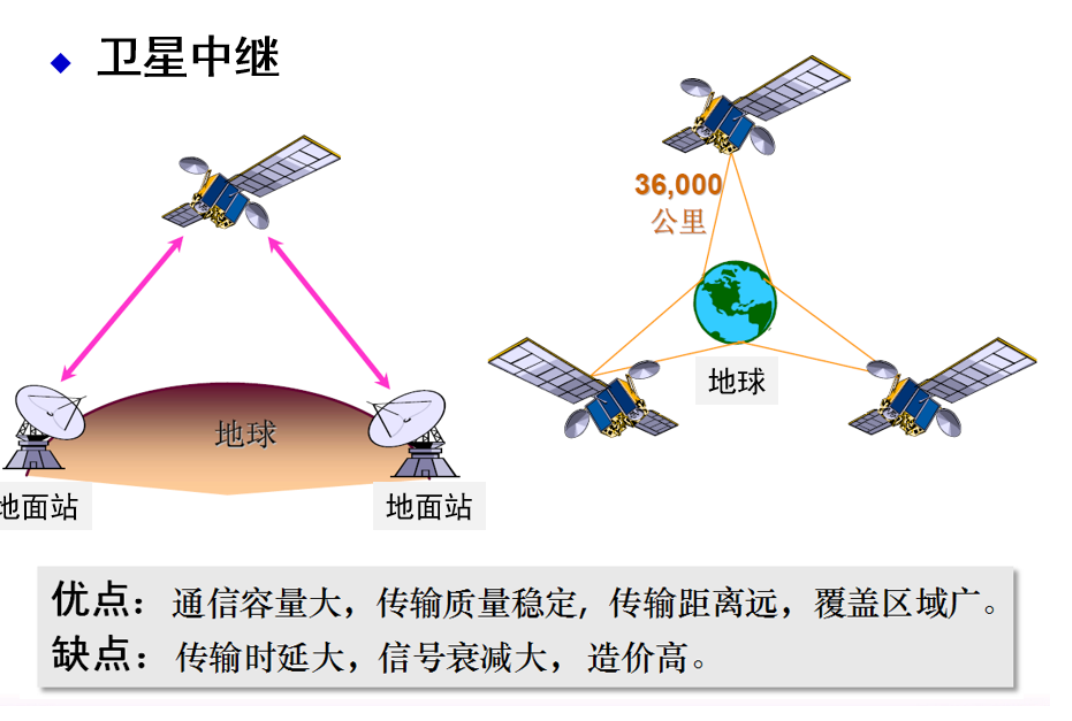
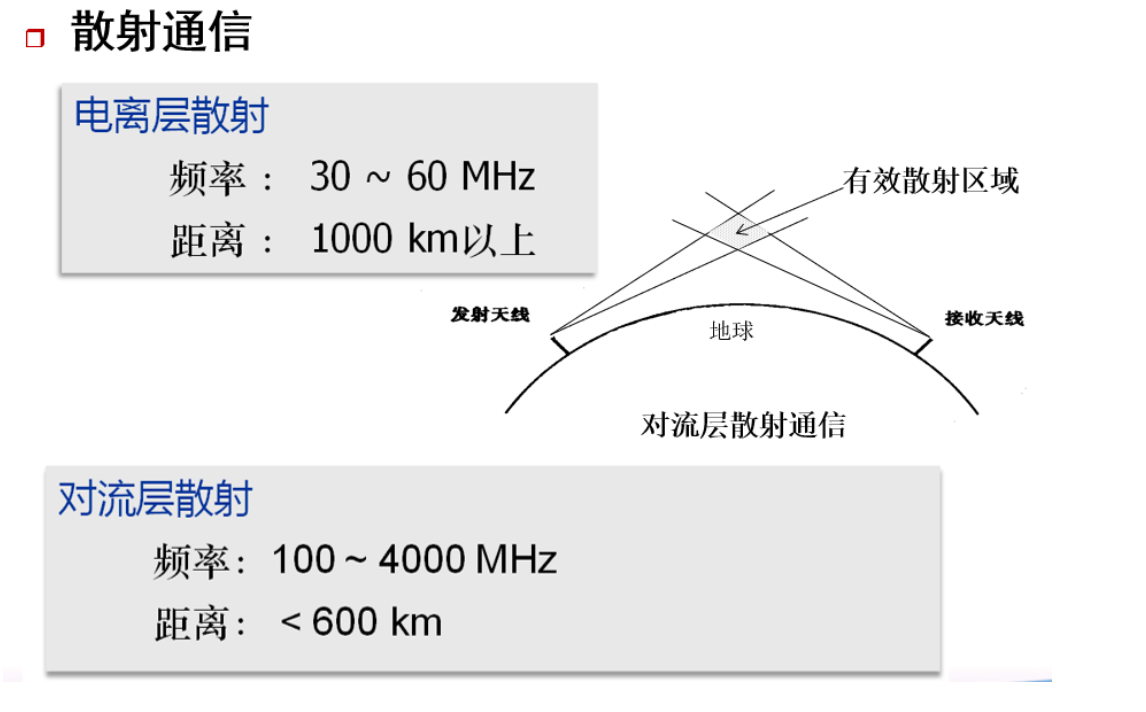
可用微波中继、卫星中继、平流层通信续费视距

微波（300M | 米波以下）

有线信道传播方式

明线、对称电缆、同同轴电缆、光纤

信道输入模型

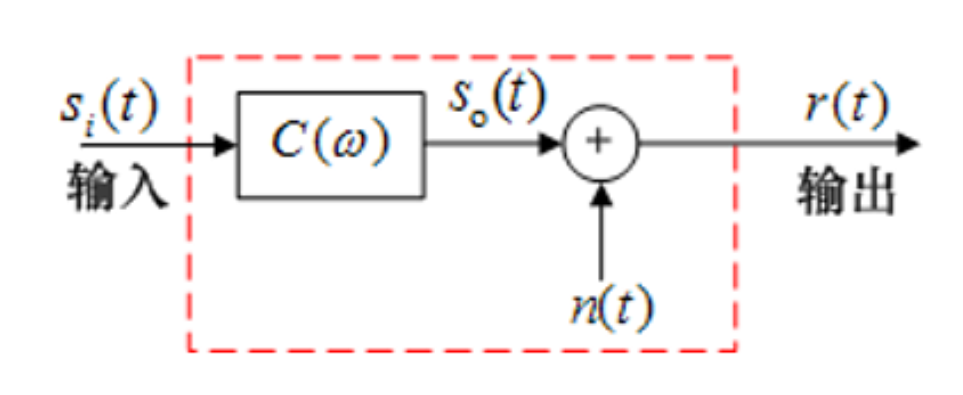
调制信道模型

调制器的输出—调制信道模型—解调器的输入

  1. 有一对（或多对）输入端和输出端
  2. 大多数信道都满足线性叠加原理
  3. 对信号有固定或时变的延迟和损耗
  4. 无信号输入时，仍可能有输出（噪声）

输入信号为

\[ r(t)=s_{o}(t)+n(t) \]

\(n(t)\) 为加性噪声

\[ s_{\scriptscriptstyle0}(t)=f[s_{i}(t)]=c(t)*s_{i}(t) \]

f 反映信道本身特征， \(c(t)\) 为乘性噪声

频域上表现为

\[ S_{\mathrm{o}}\left(\omega\right)=C(\omega)S_{\mathrm{}_{i}}(\omega) \]

根据信道的时变特性(乘性噪声是否恒定 | 是否线性时不变)，分为恒参信道和随参信道
恒参信道，又称为加性高斯白噪声信道模型

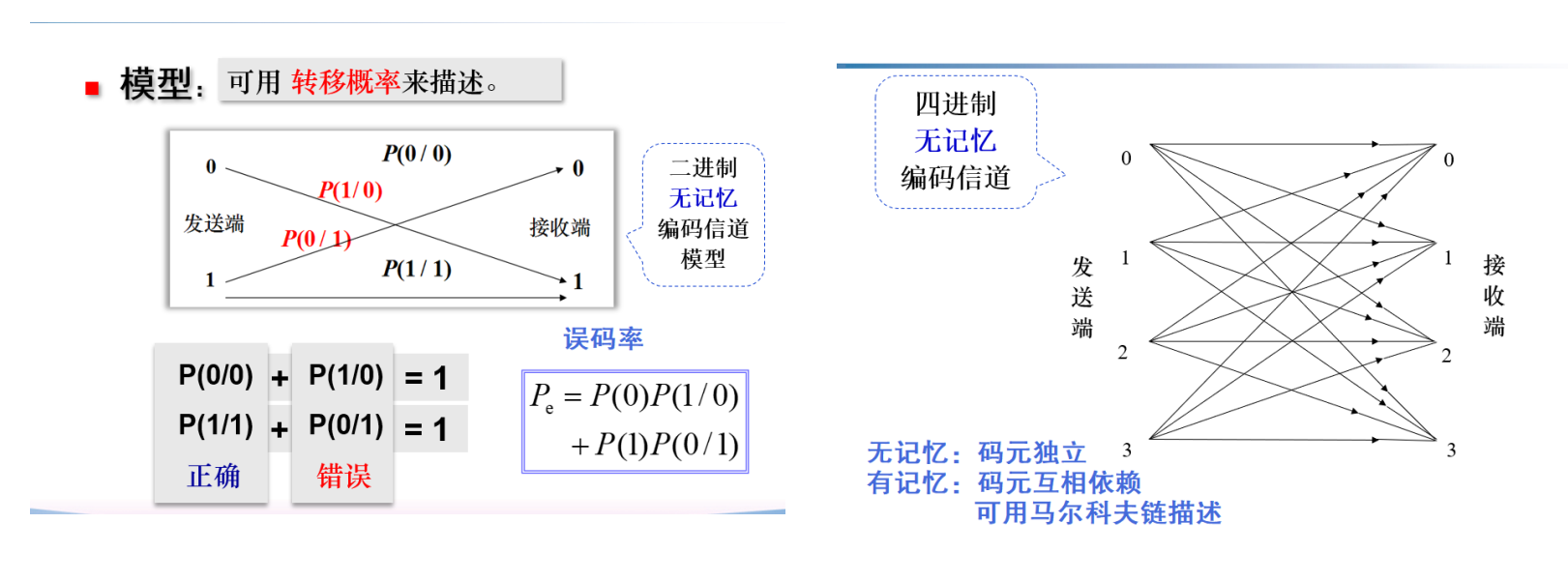
编码信道模型

转移概率：P(NextState | NowState)，为从当前状态跳转到某一状态的概率

模型用转移概率来描述

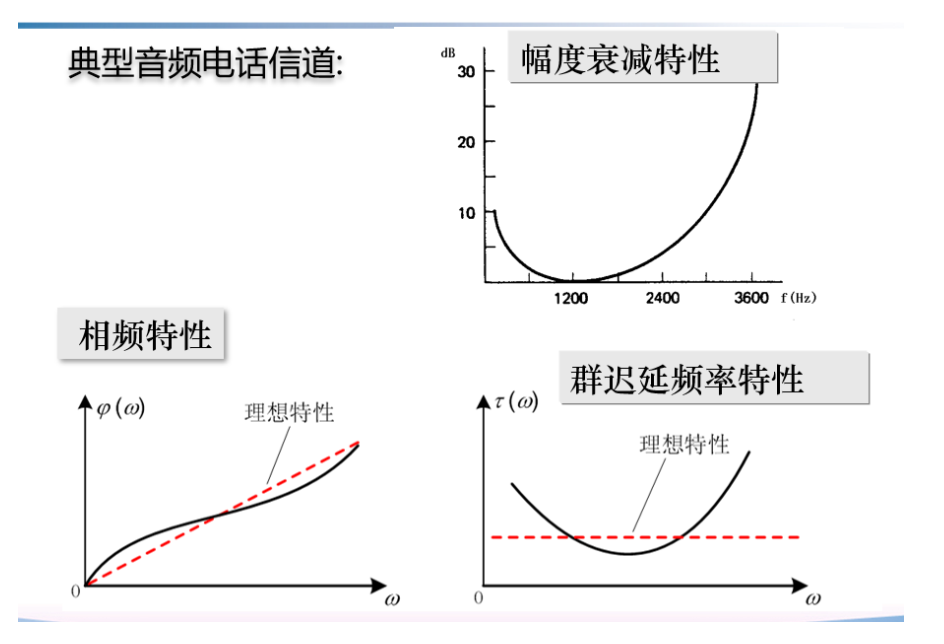
恒参信道对信号传输的影响

无失真传输特性—理想信道

  • \(H\left(\omega\right)=Ke^{-j\omega t_d}\)
  • \(\begin{array}{r}{\lvert H(\omega)\rvert=K}\\ {\varphi(\omega)=\omega\,t_{d}}\end{array}\)
  1. 系统幅频响应常数
  2. 系统相频响应线性
  3. 群迟延特性常数（不同频谱分量都为等时延迟）

失真

加性噪声引起失真

  1. 幅频失真
  • 对模拟信号：造成波形失真 \(\to\) SNR 下降
  • 对数字信号：码间串扰 \(\rightarrow\) 误码率增大
  1. 相频失真
  • 对语音信号影响不大，对视频信号影响大
  • 对数字信号：码间串扰 \(\rightarrow\) 误码率增大
  1. 群迟延失真

措施

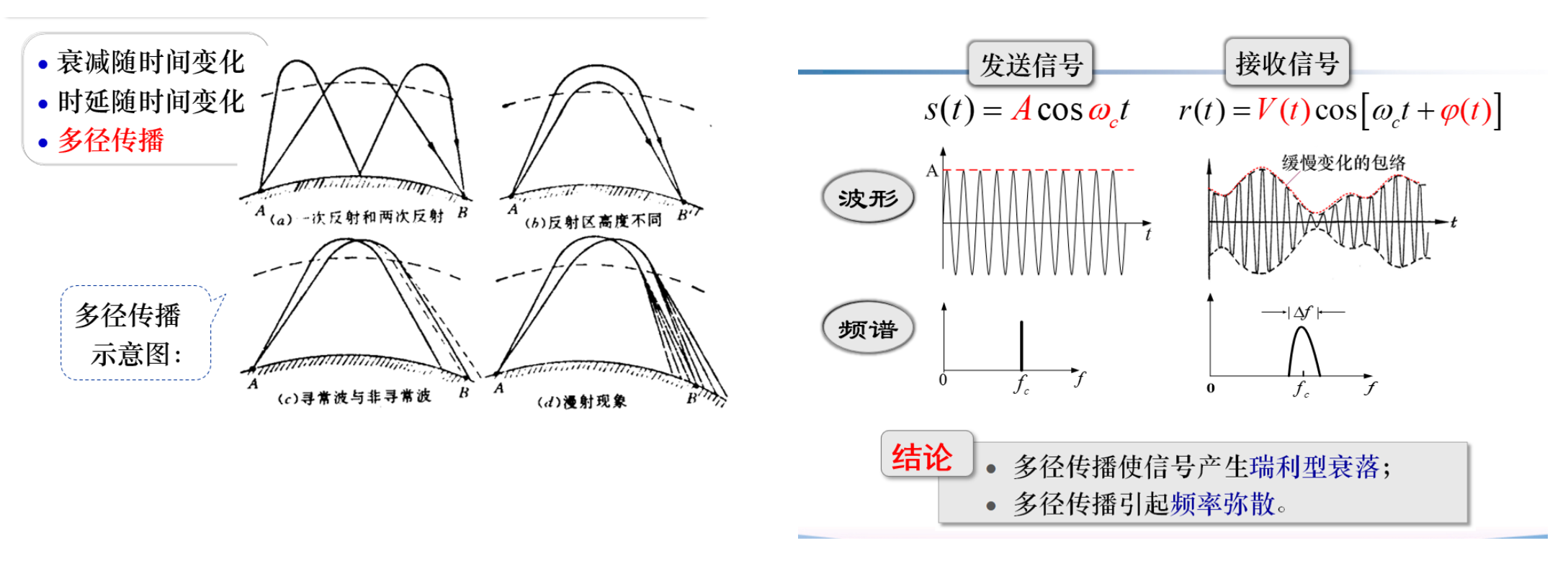
随参信道对信号传输的影响

乘性噪声随时间随机快变，引发多径效应

多径传播产生瑞利型衰落、引起频率弥散

\[ r(t)=\sum_{i=1}^{n}a_{i}(t)\cos\varphi_{i}\cos\omega_{c}t-\sum_{i=1}^{n}a_{i}(t)\sin\varphi_{i}\sin\omega_{c}t \\ =\underline{{X}}(t)\cos\omega_{c}t-\underline{{Y}}(t)\sin\omega_{c}t \\ =V(t)\cos[\omega_{c}t+\varphi(t)] \]

幅值满足瑞利分布、相位满足均匀分布

衰落

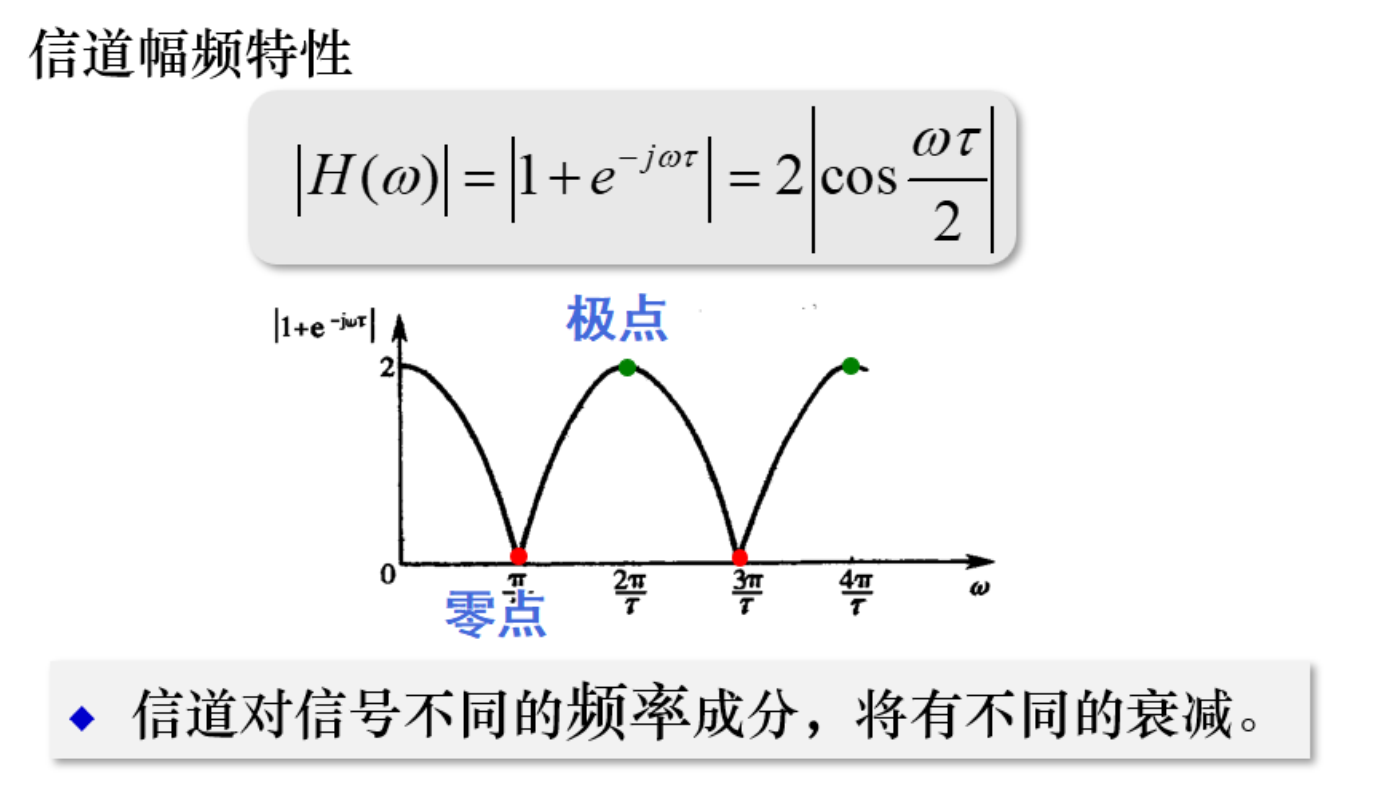
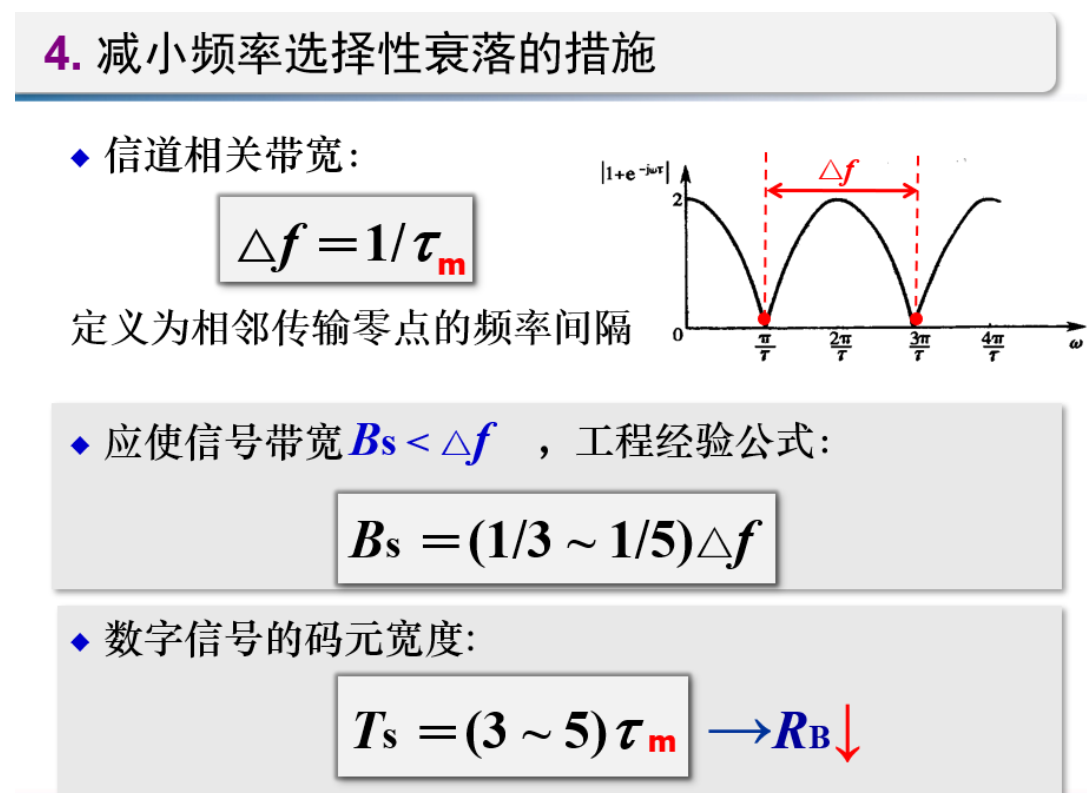
实际上只考虑俩条信道，则有信道传输函数

\[ H(\omega)=\frac{F_{0}(\omega)}{F(\omega)}={\color{blue}K} {\color{purple}e^{-j\omega x_{1}}}{\color{red}(1+e^{-j\omega x})} \]
\[ 常数衰减因子 | 确定的传输时延因子 | 信号频率 w 有关的复因子 \]

频率选择性衰落

补偿措施

总结

  • 分集
  • 扩频
  • OFDM

信道噪声

  • 按噪声来源，有人为 | 自然 | 内部噪声

  • 按性质，有脉冲 | 窄带 | 起伏噪声

热噪声—高斯白噪声

电子热运动
均匀分布在 0~1e12 Hz

电压有效值表达式

\[ \boxed{V=\sqrt{4k T R B}} \]

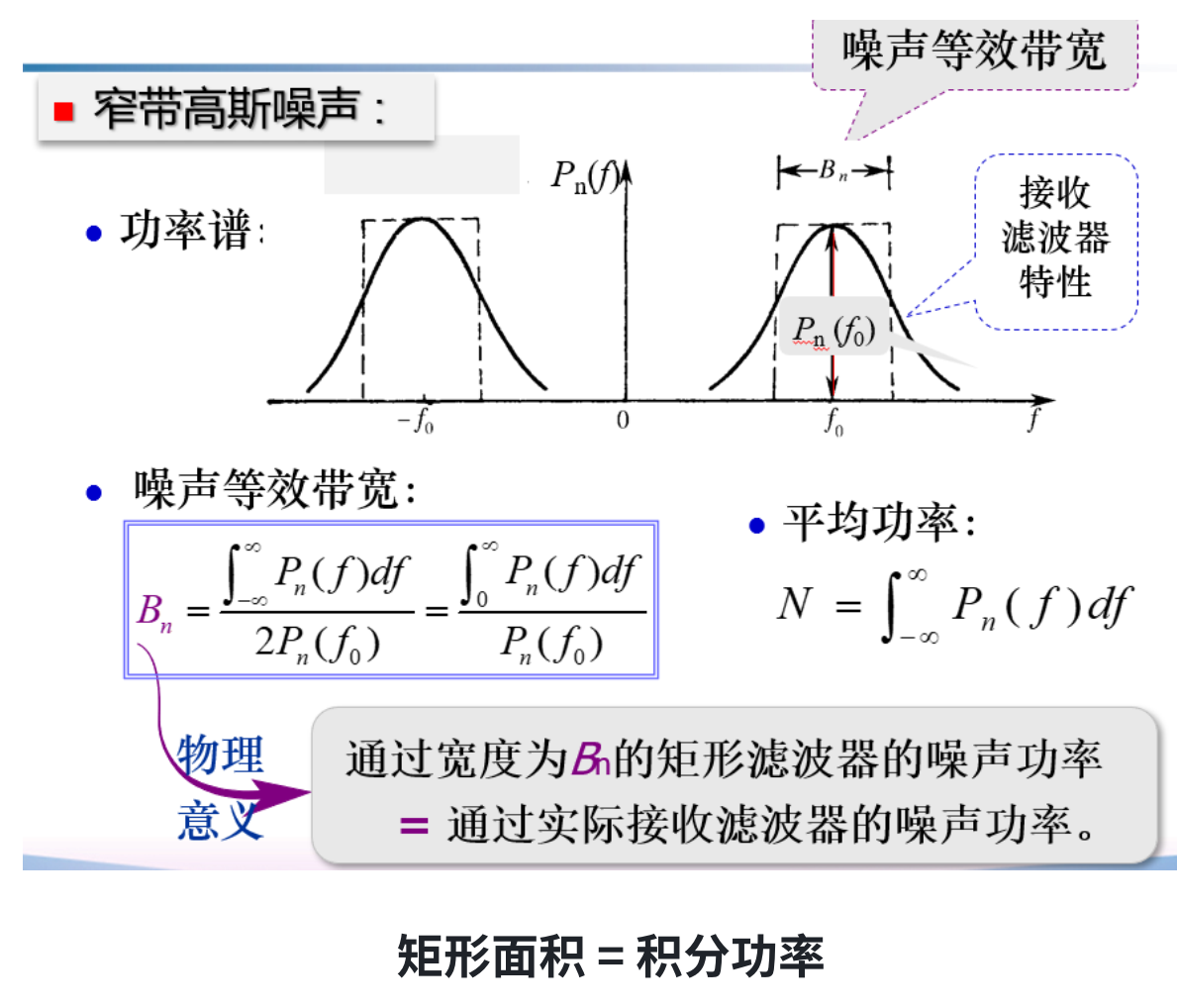
噪声等效带宽

基于功率谱密度的面积一致，找出等效噪声带宽 Bn

得到噪声等效带宽表达式

\[ B_{n}=\frac{\int_{-\infty}^{\infty}P_{n}(f)d f}{2P_{n}(f_{0})}=\frac{\int_{0}^{\infty}P_{n}(f)d f}{P_{n}(f_{0})} \]

信道容量

无差传输时的最大平均信息速率

离散信道容量

  • 信源发送熵 H(X)
\[ H(x)=-\sum_{i=1}^{n}P(x_{i})\log_{2}P(x_{i}) \]
  • 信道噪声损失熵（接收熵） \(\mathsf{H}(\mathsf{X}|\mathsf{Y})\)
\[ H(x/y)=-\sum_{i=1}^{m}P(y_{j})\color{red}\sum_{i=1}^{n}P(x_{i}/y_{j})\log_{2}P(x_{i}/y_{j}) \]

红色部分为根据转移概率推测 x 的信息量（无噪时，所有项均为 0）

\(P(y_{j})\) 为收到 \(y_{j}\) 的概率， \(P(x_{i}|y_{j})\) 为收到 \(y_{j}\) 下判断为 \(x_{i}\) 的概率

  • 信息传输速率 R (bps)
\[ \boxed{R=r\cdot\left[H(x)-H(x/y)\right]} \]

r 为每秒传输的符号数

  • 信道容量 Ct | C
\[ C_{\mathrm{t}}=\operatorname*{max}_{P(x)}\{R\}=\operatorname*{max}_{P(x)}\{r[H(x)-H(x/y)]\}\;(\mathrm{b/s}) \]

去掉时间参量，等价为

\[ C=\max_{P(x)}[H(x)-H(x/y)]\mathrm{~(}b/\text{符号)} \]

连续信道容量

包含带宽与 SNR

香农定理—单发单收下

\[ \boxed{C=B\log_{2}\left(1+\frac{S}{N}\right)=B\log_{2}\left(1+\frac{S}{n_{0}B}\right)\,\left(\mathrm{b/s}\right)} \]
  • 若 \(\mathsf{R b\!\leqslant\!C}\) ，则总能找到一种信道编码方式，实现无差错传输
  • 若传输速率大于信道容量，则不可能实现无差错传输

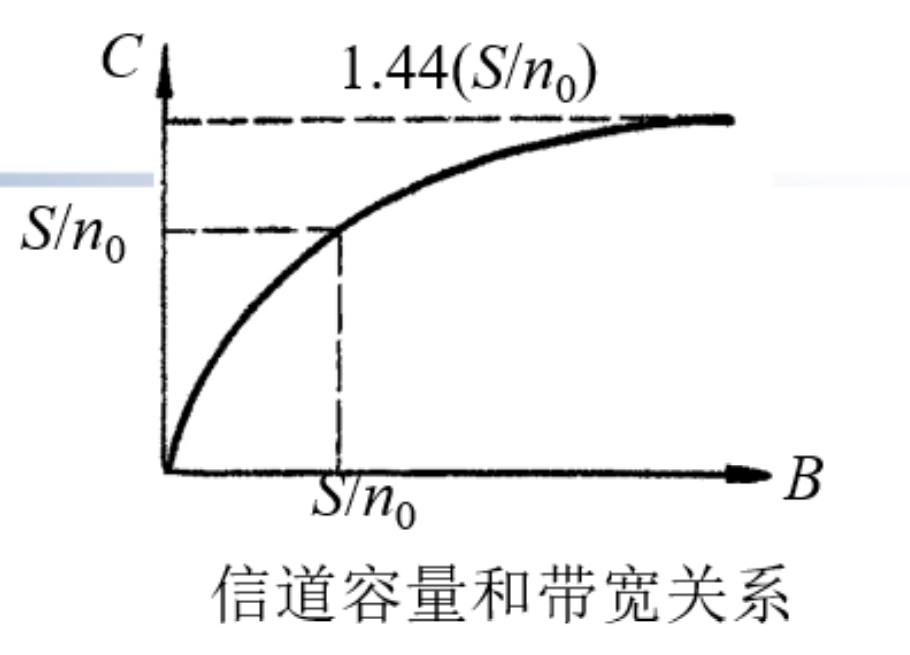
性质

  • S↑ 或者 n↓，则 \(\mathbf{c}{\rightarrow}\infty\)
  • B↑ 而 C 收敛
\[ \operatorname*{lim}_{B\to\infty}C=\operatorname*{lim}_{B\to\infty}B\log_{2}(1+{\frac{S}{n_{0}B}})={\frac{S}{n_{0}}}\log_{2}e\approx1.44{\frac{S}{n_{0}}} \]

例

例 | 以像素为单位

已知彩色电视图像画面由 \(5\times10^{5}\) 个像素组成。设每个像素有 64 种彩色度。每种彩色度有 16 个亮度等级。如果所有彩色度和亮度等级的组合机会均等，并统计独立

  1. 试计算每秒传送 100 幅画面所需的信道容量
  2. 如果接收机信噪比为 30dB，为了传送彩色图像所需信道带宽为多少？