幅度调制
调制与解调
调制:把消息信号搭载到载波的某个参数上
解调:把基带信号从载波中恢复信号
调制作用
- 频谱搬移,缩减天线长度,改善性能
- 信道区分,多路复用,避免干扰
信号类型
- 调制信号(基带信号) \(m(t)\)
- 载波 \(c(t)\)
- 已调信号 \(s(t)\)
\(1\leftrightarrow2\pi\delta(w)\) 等价为 \(\delta(f)\)
调制方式
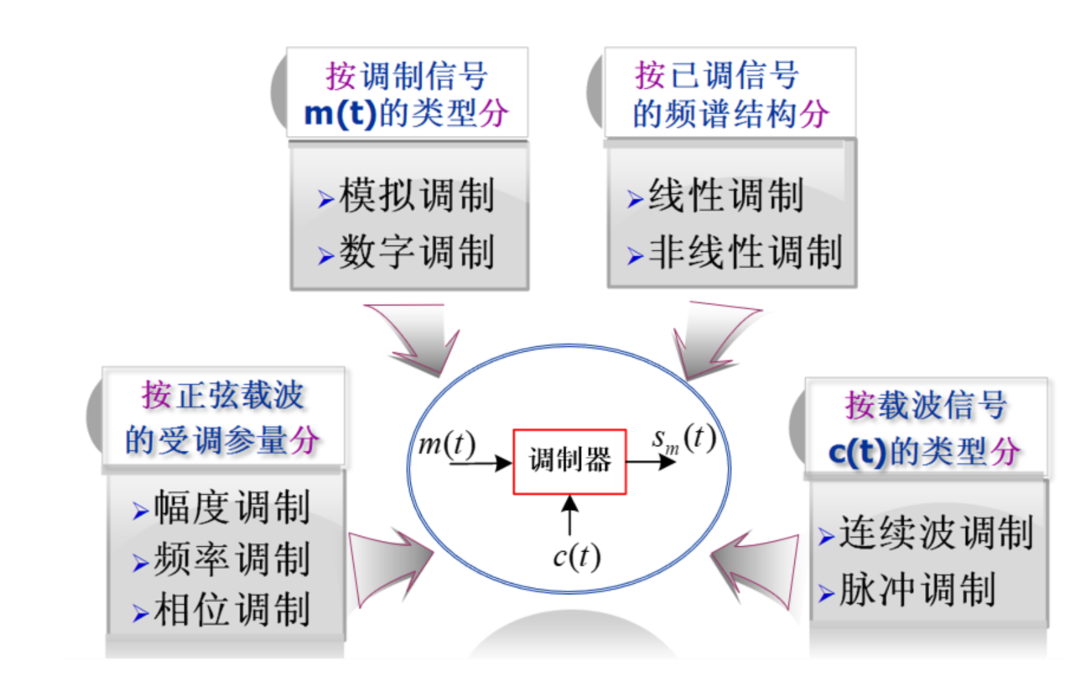
- 幅度(线性)调制方式:AM、DSB、SSB、VSB,取决于边带滤波器
- 角度(非线性)调制:FM、PM
线性调制原理
原理框图
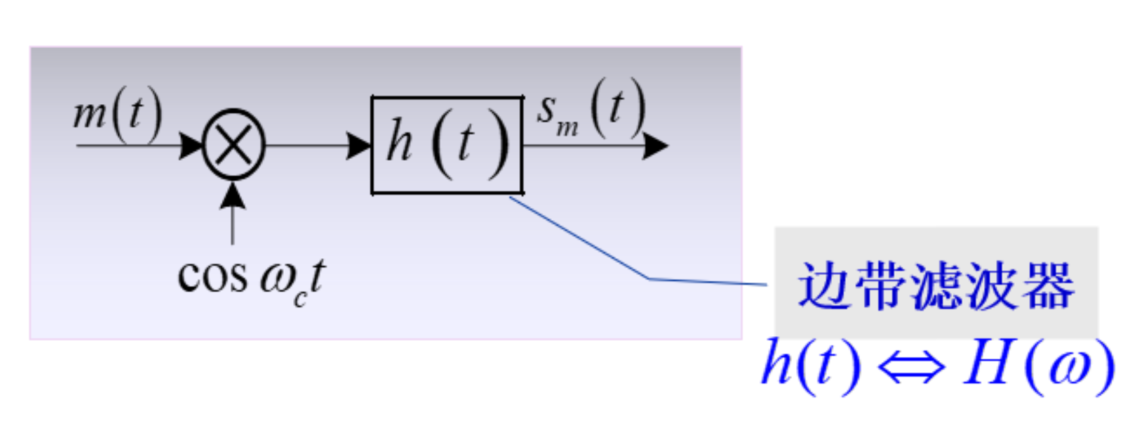
- 时域下的已调信号: \(s_{m}(t)=[m(t)\cos\omega_{c}t]*h(t)\)
- 频域下: \(S_{m}(\omega)=\frac{1}{2}[M(\omega+\omega_{c})+M(\omega-\omega_{c})]H(\omega)\)
AM
调制框图
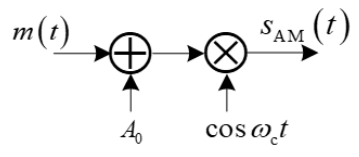
前置条件
- 偏置前均值为 0
- 基带信号加偏置,使之为直流信号(全都为正)
表达式
\[
s_{\mathrm{AM}}\left(t\right)=\left[A_{0}+m(t)\right]\cos\omega_{\mathrm{c}}t=A_{0}\cos\omega_{\mathrm{c}}t+m(t)\cos\omega_{\mathrm{c}}t
\]
前者为载波项,后者为边带项
频域下有
\[
S_{\mathrm{AM}}(\omega)=\pi A_{0}\left[\delta(\omega+\omega_{\mathrm{c}})+\delta(\omega-\omega_{\mathrm{c}})\right]+\frac{1}{2}\left[M(\omega+\omega_{\mathrm{c}})+M(\omega-\omega_{\mathrm{c}})\right]
\]
表现为上下边带 + 载波直流分量(不要的)
调制前后波形为
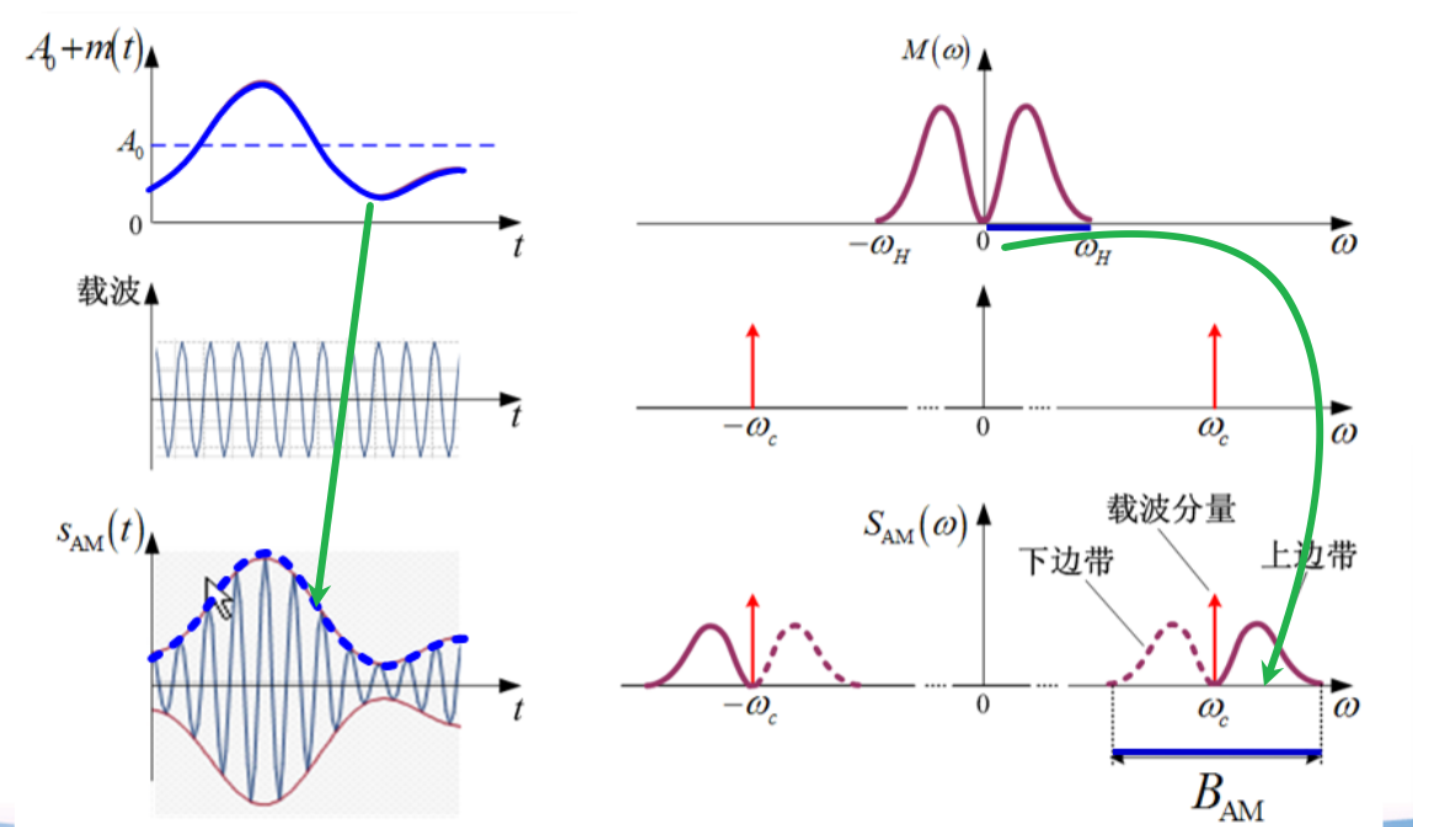
传输带宽 \(B_{A M}=2f_{H}\)
只有幅值变化,故称为线性调制
AM 小结
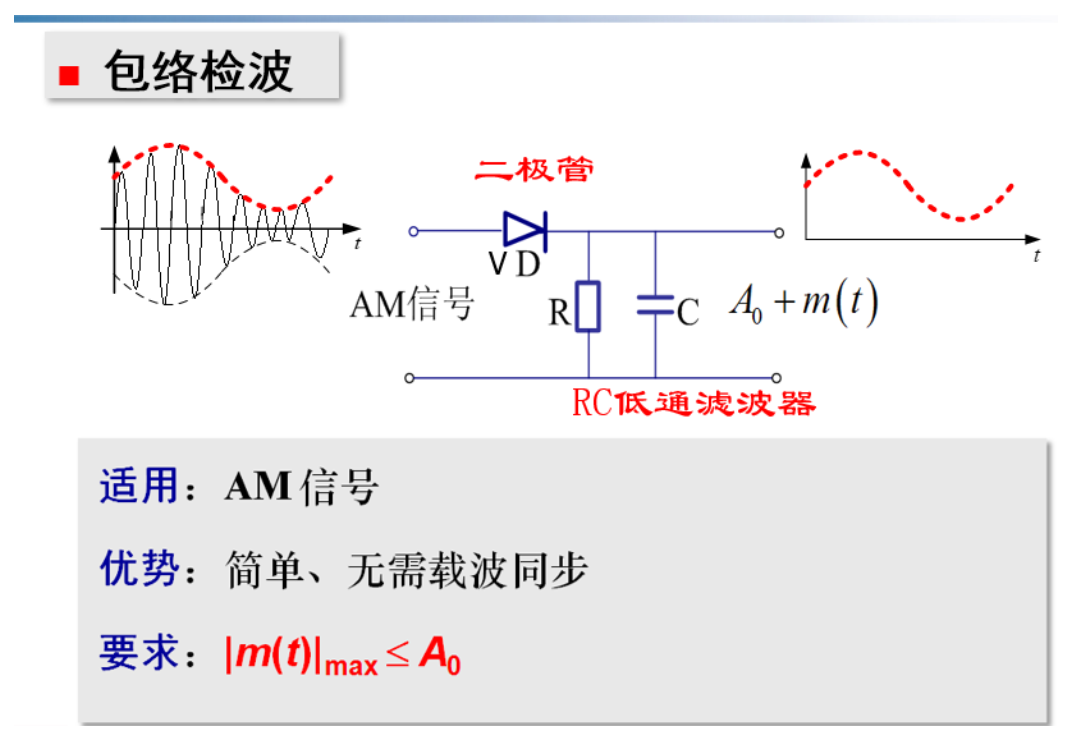
- \(\left|m\!\left(t\right)\right|_{\mathrm{max}}\leq A_{0}\) 时,AM 波的包络正比于调制信号 \(m(t)\) ,故可采用包络检波。
- AM 的频谱由载频分量、上边带和下边带组成。
- AM 传输带宽是调制信号带宽的两倍:\(\boxed{B_{\mathrm{AM}}=2f_{H}}\)
- AM 的优势在于接收机简单,广泛用于中短调幅广播。
鲁迅说过:看着简单的东西往往都有麻烦的问题
观察功率(即均方值)
发现直流量使调制效率低
\[
s_{\mathrm{AM}}\left(t\right)=A_{0}\cos\omega_{c}t+m\left(t\right)\cos\omega_{\mathrm{c}}t
\]
AM 信号功率
\[
P_{\mathrm{{AM}}}={\frac{A_{0}^{2}}{2}}+\frac{\overline{{{m^{2}(t)}}}}{2}=P_{c}\;+\;P_{s}
\]
调制效率(功率利用率)
\[
\boxed{\eta_{\mathrm{{AM}}}=\frac{P_{\mathrm{{s}}}}{P_{\mathrm{{AM}}}}\!=\!\frac{\overline{{m^{2}(t)}}}{A_{0}^{2}+\overline{{m^{2}(t)}}}}
\]
\(\left|m(t)\right|_{\mathrm{max}}\leq A_{0}\) . \(.m^{2}(t)\leqslant{A_{0}}^{2}\) 故 \(\eta_{\mathrm{AM}}\leqslant50\%\)
即载波项不含有有用信息,却浪费发射功率
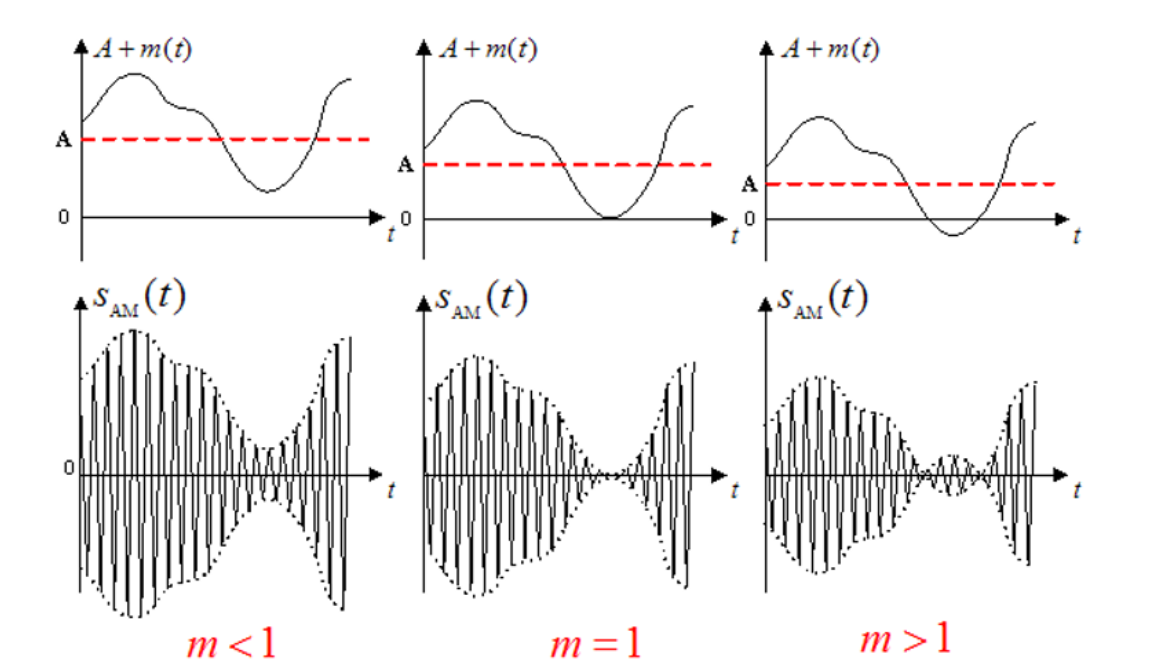
定义:调幅度
反映基带信号改变载波幅度的程度,表现为已调信号的起伏
\[
m=\frac{|m(t)|_{\mathrm{max}}}{A_{0}}=\frac{A_{m}}{A_{0}}
\]
令基带信号为单音正弦信号 \(m(t)=A_{m}\cos\omega_{m}t\) ,则 \(\overline{{m^{2}\left(t\right)}}=A_{m}^{2}/2\)
此时
\[
\eta_{\mathrm{AM}}={\frac{A_{m}^{2}}{2A_{0}^{2}+A_{m}^{2}}}={\frac{A_{m}^{2}\left/\ A_{0}^{2}\right.}{2+A_{m}^{2}\left/\ A_{0}^{2}\right.}}={\frac{m^{2}}{2+m^{2}}}
\]
满调幅时效率最高,为1/3
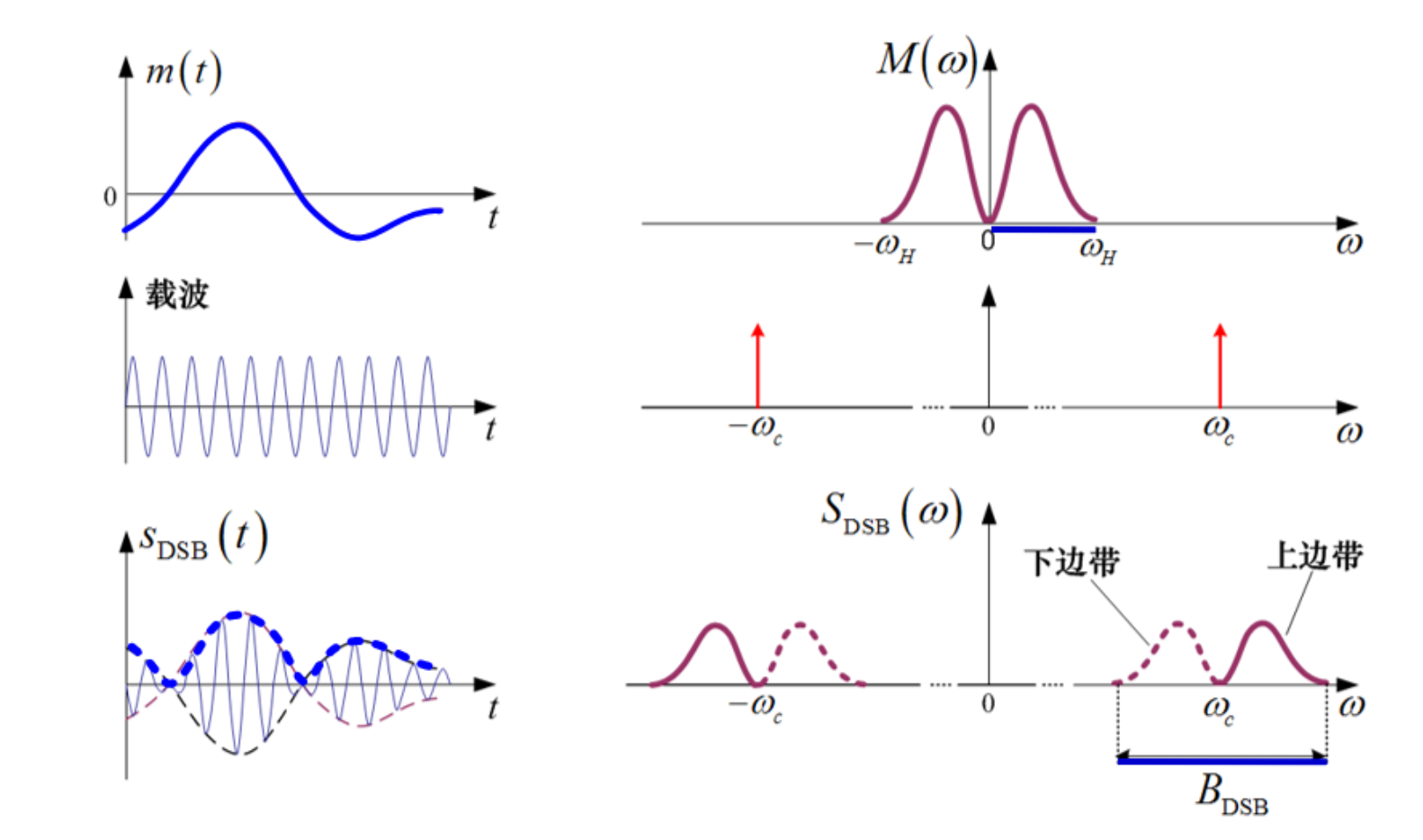
DBS-SC
调制框图
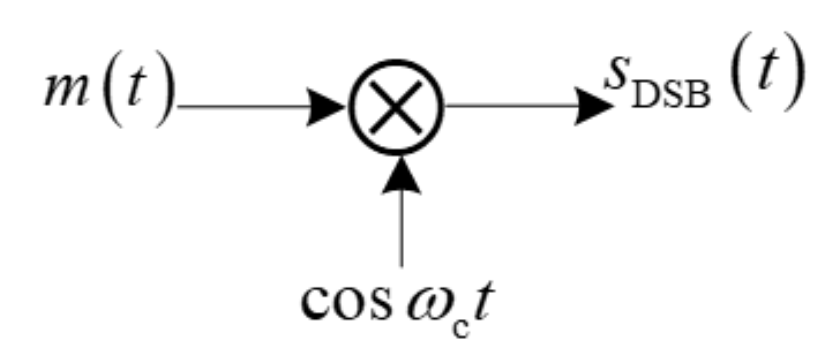
表达式
直接与载波相乘
\[
s_{\mathrm{AM}}\left(t\right)=m(t)\cos\omega_{\mathrm{c}}t
\]
频域下
\[
S_{\mathrm{DSB}}(\omega)=\frac{1}{2}\Big[M(\omega+\omega_{\mathrm{c}})+M(\omega-\omega_{\mathrm{c}})\Big]
\]
此时接收机不能使用包络检波(载波在过零点倒相,包络为原信号上翻整流结果)
DSB 小结

让带宽占用更少一些,进一步只考虑单边带
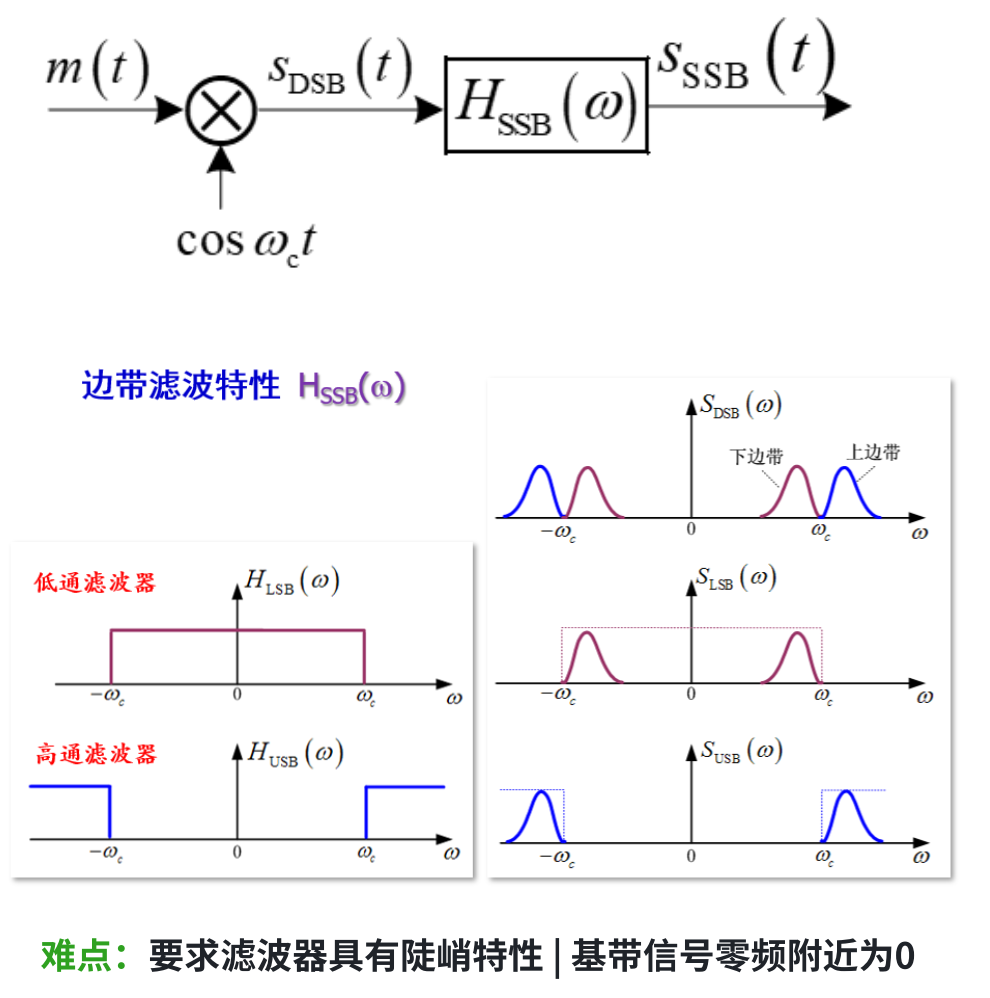
SSB
单边带调制
有滤波法、相移法俩种方法
设
\[
\begin{aligned}s_{DSB}(t)&=A_m\cos\omega_mt\cdot\cos\omega_ct\\&={\color{red}\frac{1}{2}A_m\cos(\omega_c-\omega_m)t}+{\color{blue}\frac{1}{2}A_m\cos(\omega_c+\omega_m)t}\end{aligned}
\]
其中,加号左边项为下边带,右边为上边带
将基带信号变为 m(t)
\[
s_{\mathrm{SSB}}\left(t\right)=\frac{1}{2}m\left(t\right)\cos\omega_{c}t\,\pm\,\frac{1}{2}\hat{m}\left(t\right)\sin\omega_{c}t
\]
正为下边带,负为上边带(三角函数 cos 展开)
其中, \(\hat{m}(t)\) 为 \(m(t)\) 的 希尔伯特变换
此处的含义为相移\(\frac{\pi}{2}\)
希尔伯特变换
对某一信号,若希望将双边谱改为单边谱,则可以将原频谱的两倍与阶跃信号相乘,即
\[
{\widetilde{X}}(f)=2\cdot X(f)\cdot U(f)
\]
对上式做逆变换,得时域谱
\[
\begin{array}{c}{{\tilde{x}(t)=2\cdot x(t)*\displaystyle\frac{1}{2}(j\displaystyle\frac{1}{\pi t}+\delta(t))}}\\ {{=x(t)+j(x(t)*\displaystyle\frac{1}{\pi t})}}\end{array}
\]
其中,将 x(t)*1/πt 定义为希尔伯特变换,即
\[
\hat{x}(t)=x(t)*\frac{1}{\pi t}
\]
那么单边解析信号又可写为
\[
\tilde{x}(t)=x(t)+j\hat{x}(t)
\]
转换框图与小结
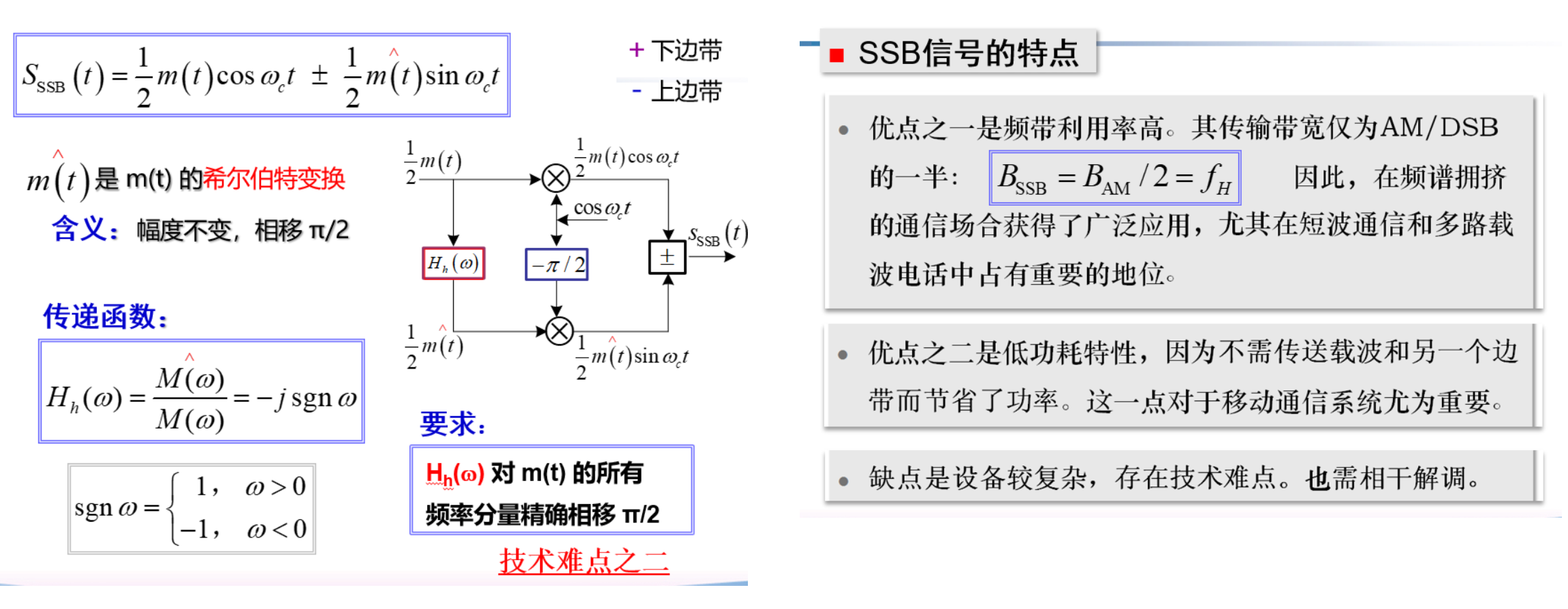
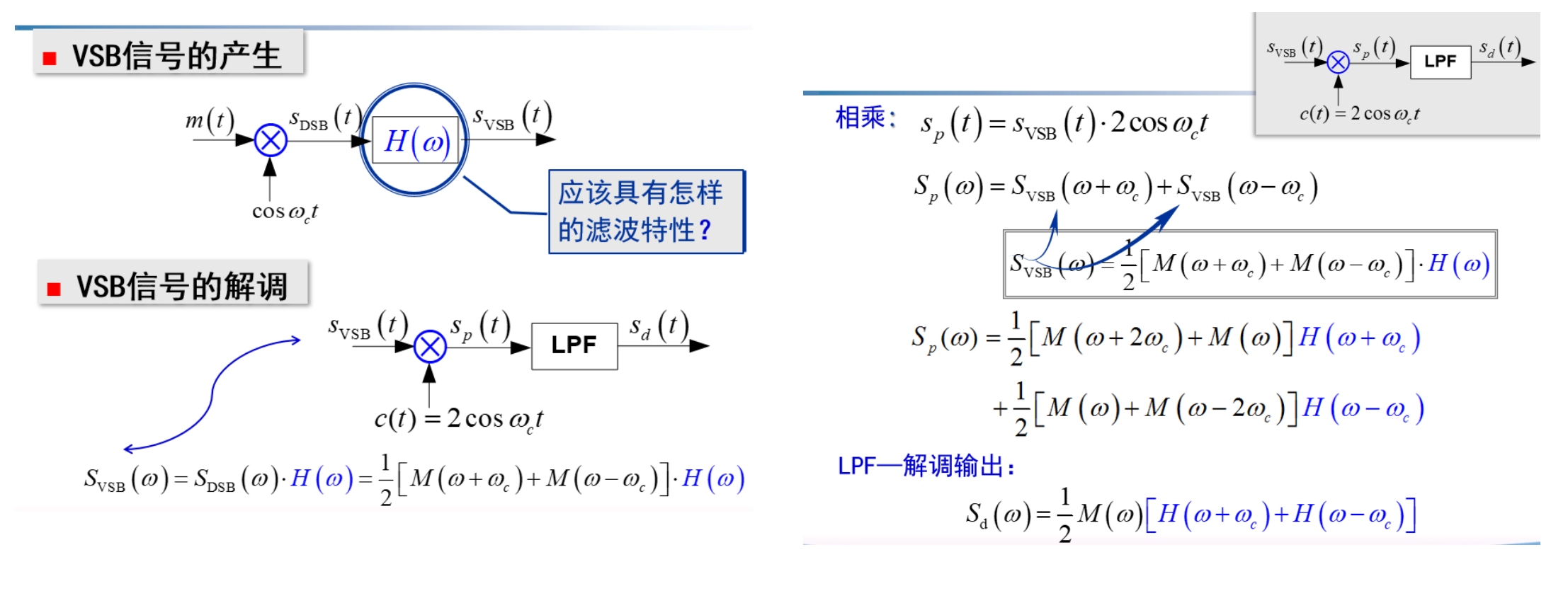
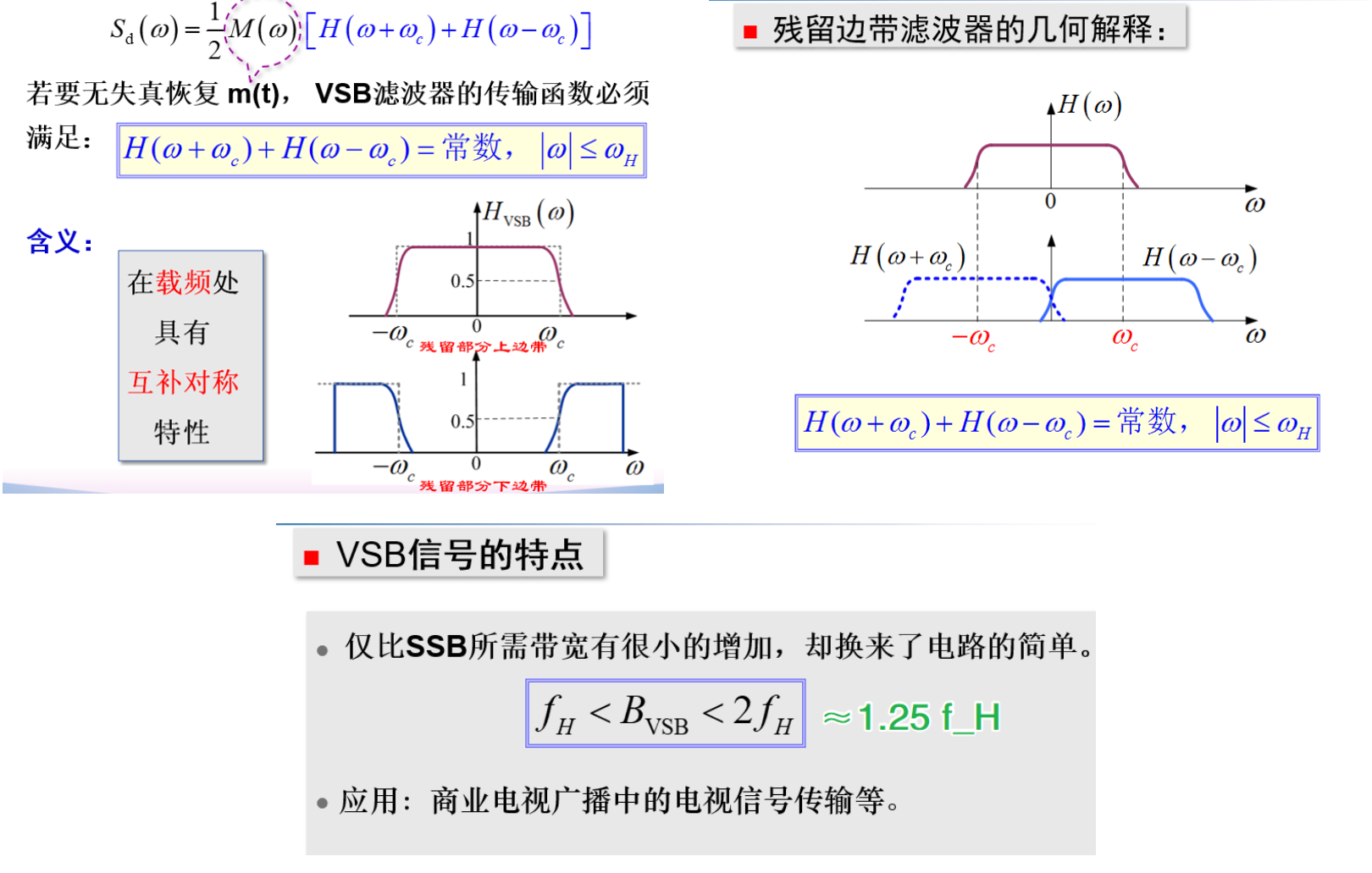
VSB
残留边带调制
一介于 SSB 与 DSB 之间的折中方案
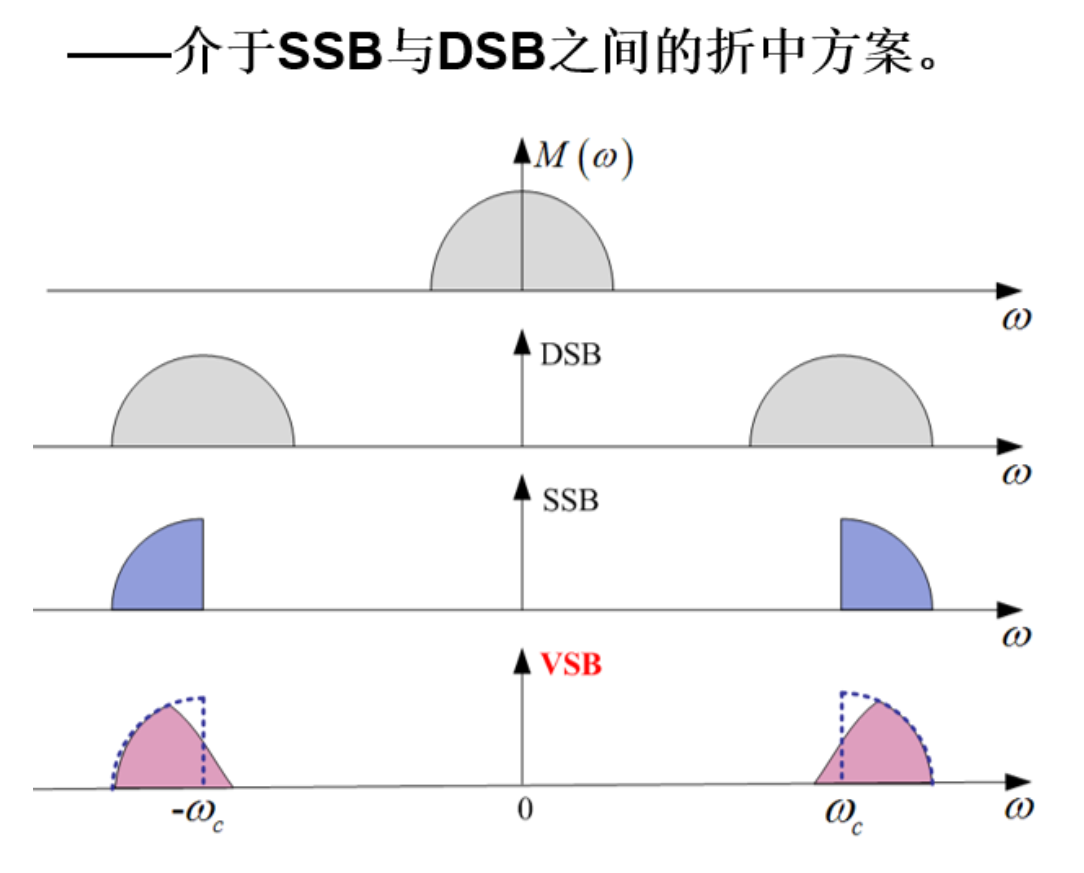
VSB 信号的产生与解调
边带滤波器性质
在 \(\pm\;\omega_{c}\) 处必须具有互补对称(奇对称)特性,即一个边带的损失恰能被另一个边带补偿
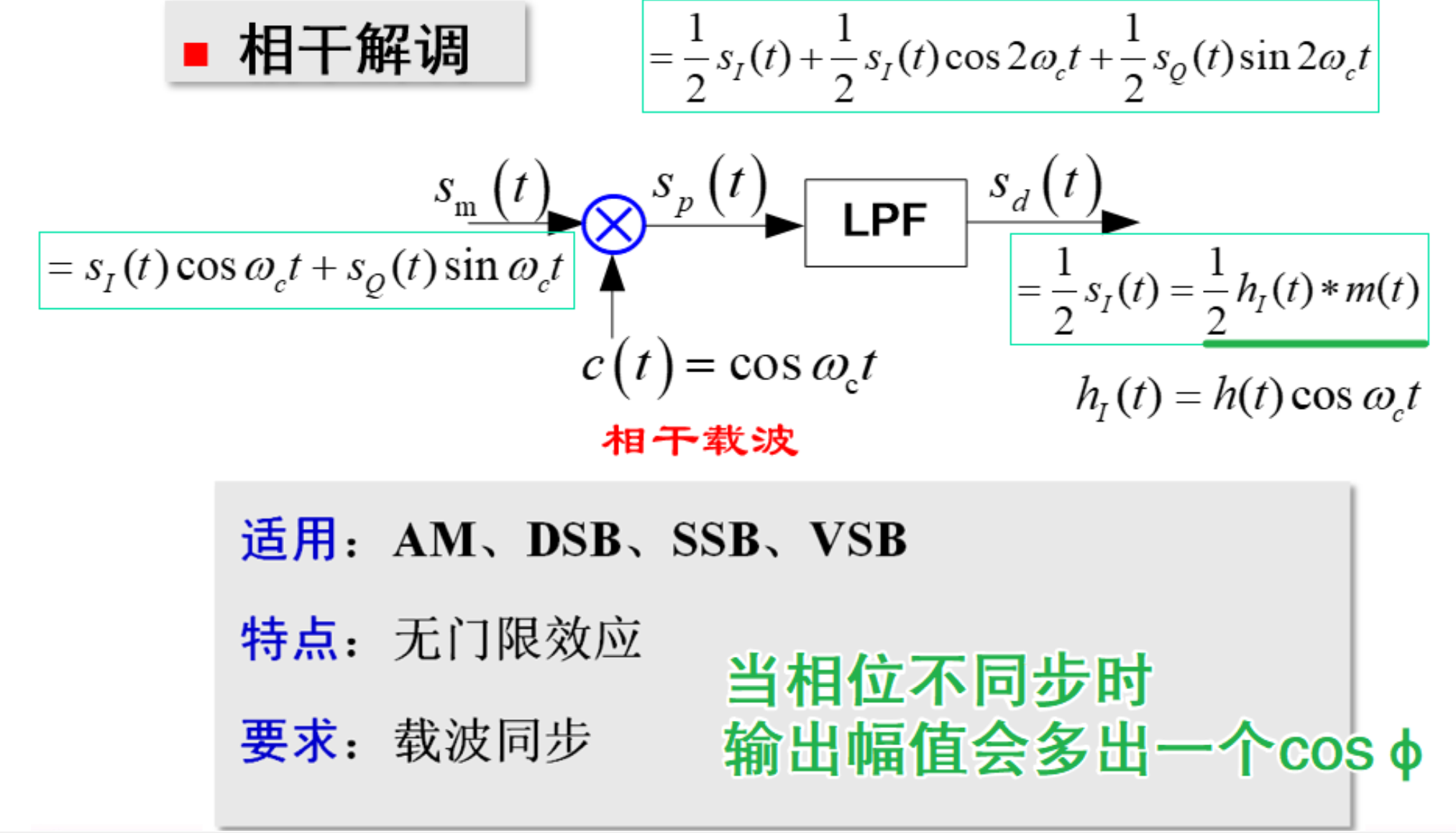
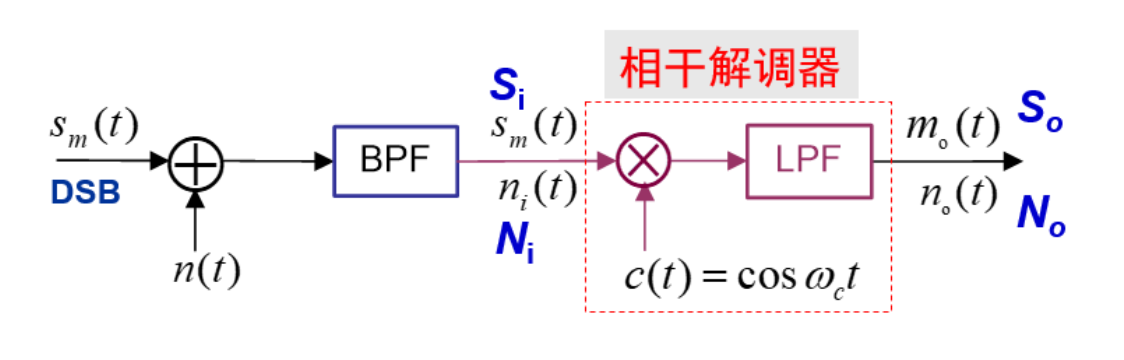
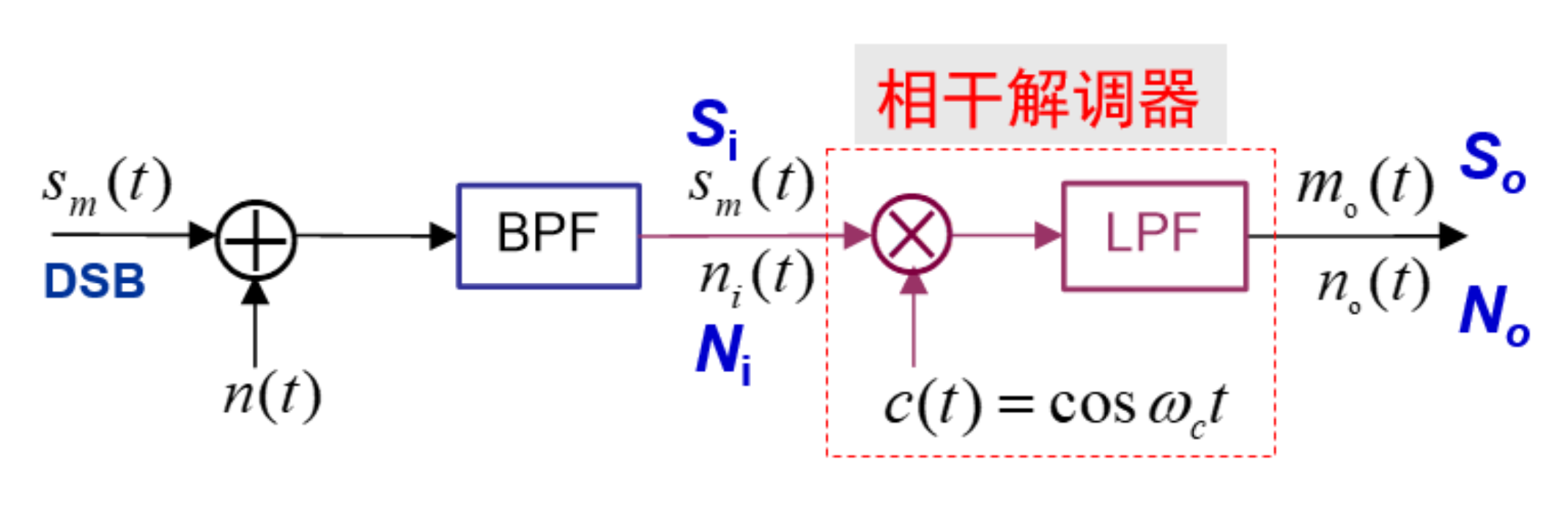
相干解调与包络检波
接收端解调
相干解调
通常用 PLL 进行相干解调
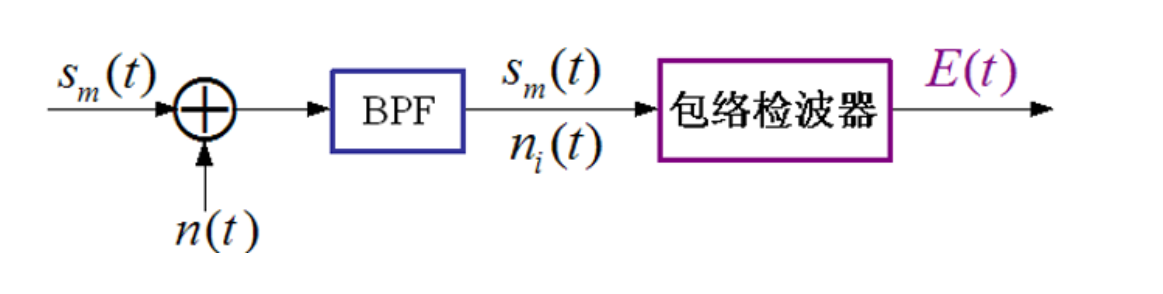
包络检波
峰值检测
插入载波包络检波法
通过大载波抬升,使得满足包络检波
小结

线性调制系统的抗噪声性能
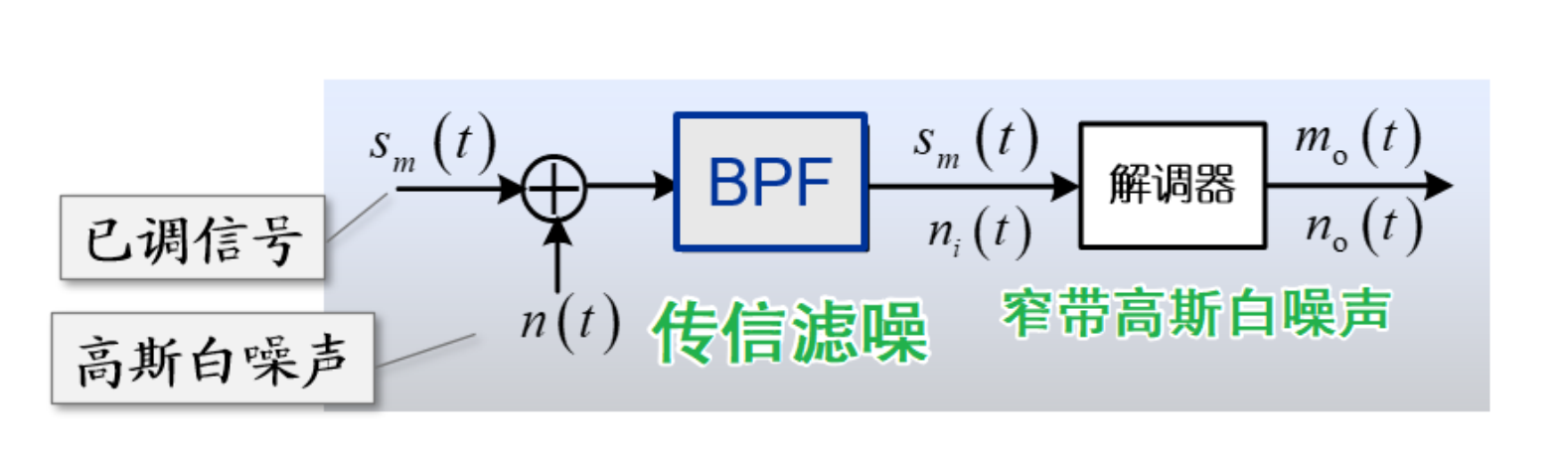
抗噪声性能的一般模型与指标
其中,窄带噪声可表示为同向分量与正交分量,有
\[
\begin{array}{r}{n_{\mathrm{i}}(t)=n_{\mathrm{c}}(t)\cos\omega_{0}t-n_{\mathrm{s}}(t)\sin\omega_{0}t}\\ {n_{\mathrm{i}}^{2}(t)=\overline{{n_{\mathrm{c}}^{2}(t)}}=\overline{{n_{\mathrm{s}}^{2}(t)}}=N_{\mathrm{i}}=n_{0}B}\end{array}
\]
BPF 的中频与带宽
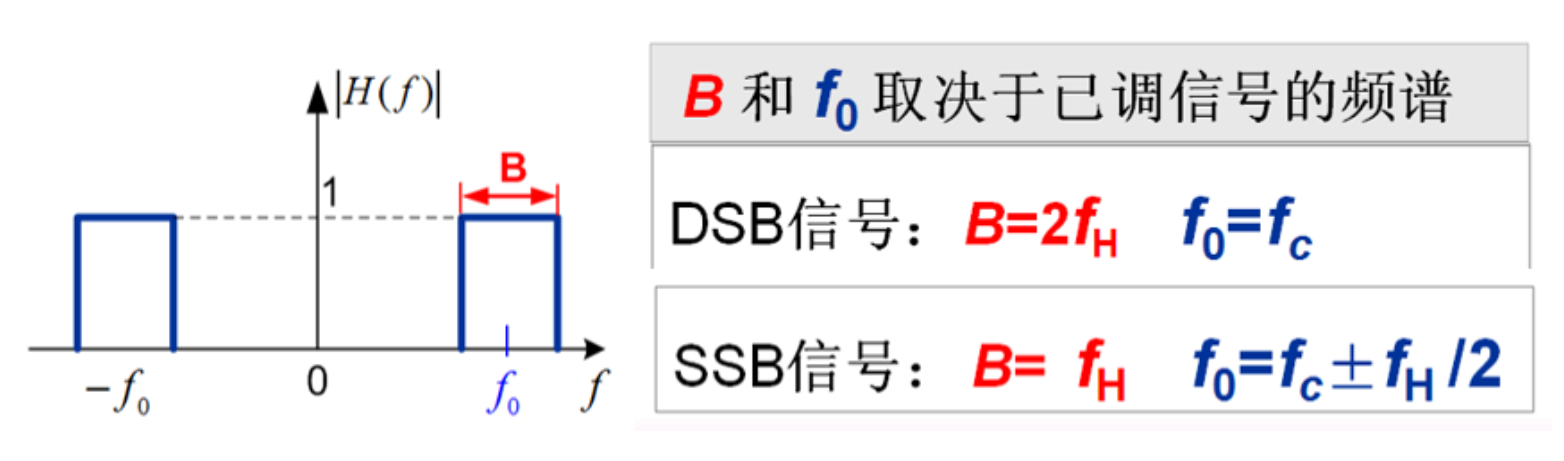
性能指标
DSB 相干解调下抗噪声性能
接收已调信号为
\[
s_{m}(t)=m(t)\cos\omega_{c}t
\]
计算均方值(功率)
\[
S_{\mathrm{i}}=\overline{{s_{m}^{2}(t)}}=\overline{{\left[m(t)\cos\omega_{\mathrm{c}}t\right]^{2}}}=\frac{1}{2}\overline{{m^{2}(t)}}
\]
又有经过相干解调的输出信号(回忆搬回零频)
\[
m_{o}(t)=\frac{1}{2}m(t)
\]
得到输出功率
\[
S_{o}=\overline{{m_{o}^{2}(t)}}=\frac{1}{4}\overline{{m^{2}(t)}}
\]
现再考虑噪声
\[
n_{\mathrm{i}}(t)=n_{\mathrm{c}}(t)\cos\omega_{0}t-n_{\mathrm{s}}(t)\sin\omega_{0}t
\]
\[
N_{i}=n_{0}B\quad B=2f_{H}
\]
窄带高斯噪声也与 cos 相乘,得
\[
n_{o}(t)=\frac{1}{2}n_{c}(t)
\]
然后 duangduang~
\[
N_{o}=\overline{{n_{o}^{2}(t)}}=\frac{1}{4}\overline{{n_{\mathrm{c}}^{2}(t)}}=\frac{1}{4}\overline{{n_{\mathrm{i}}^{2}(t)}}=\frac{1}{4}\,N_{\mathrm{i}}
\]
所以得到结论
\[
\boxed{\begin{array}{c}S_{\mathrm{i}}=\frac{1}{2}\overline{m^{2}\left(t\right)}\\\\N_{\mathrm{i}}=n_{0}B\end{array}}\boxed{\begin{array}{c}S_{\mathrm{o}}=\frac{1}{4}\overline{m^{2}\left(t\right)}\\\\N_{\mathrm{o}}=\frac{1}{4}N_{\mathrm{i}}\end{array}}
\]
信号“衰减”½,噪声“衰减”¼
即
\[
G_{DSB}=2
\]
改善原因
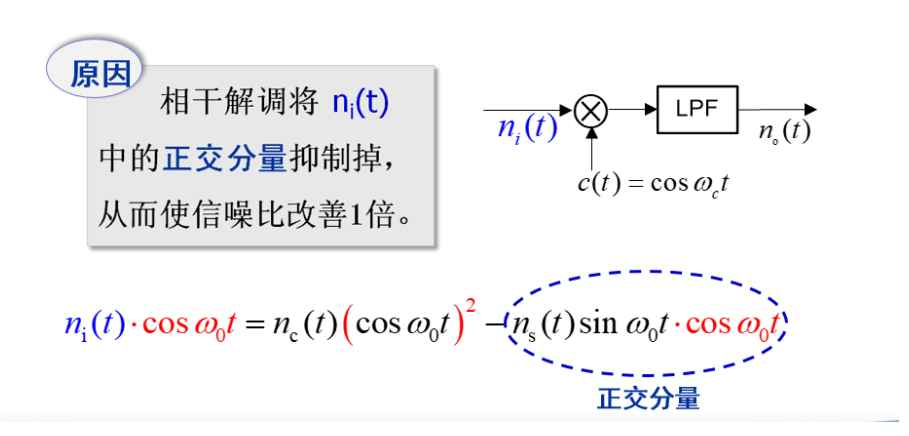
SSB 相干解调下抗噪声性能
\[
s_{m}(t)=\frac{1}{2}m(t)\cos\omega_{c}t\pm\frac{1}{2}\hat{m}(t)\sin\omega_{c}t
\]
\[
m_{0}(t)=\frac{1}{4}m(t)
\]
同时,噪声不变
得到结果
\[
\boxed{\begin{array}{ll}S_\mathrm{i}=\frac{1}{4}\overline{m^2(t)}&S_\mathrm{o}=\frac{1}{16}\overline{m^2(t)}\\\\N_\mathrm{i}=n_0B&N_\mathrm{o}=\frac{1}{4}N_\mathrm{i}\end{array}}
\]
信号“衰减” ¼ ,噪声“衰减”¼
\[
G_{S S B}=1
\]
因为 SSB 同时抑制了信号与噪声的正交分量,故制度增益没有变化

AM 包络检波下抗噪性能
令输入已调信号为
\[
s_{m}\left(t\right)+n_{\mathrm{i}}\left(t\right)=\left[A_{0}+m\left(t\right)+n_{\mathrm{c}}\left(t\right)\right]\cos\omega_{\mathrm{c}}t-n_{\mathrm{s}}\left(t\right)\sin\omega_{\mathrm{c}}t
\]
其中,检波信号与加性噪声与其功率分别为
注意这里默认分母的 \({\mathsf{R}}{=}{\mathsf{1}}{\Omega}\)
\[
s_{\mathrm{AM}}(t)=[A_{0}+m(t)]\cos\omega_{c}t~~~~S_{i}=\frac{A_{0}^{2}}{2}+\frac{\overline{{m^{2}\left(t\right)}}}{2}
\]
\[
n_{\mathrm{i}}(t)=n_{\mathrm{c}}(t)\,\cos\omega_{0}\,t\,-n_{\mathrm{s}}(t)\sin\omega_{0}\,t\,\quad\,N_{\mathrm{i}}=n_{0}B
\]
和角简化后可以得到
\[
E(t)\mathrm{cos}\Big[\omega_{c}t+\varphi(t)\Big]
\]
合成包络 \(E(t)\)
\[
E\left(t\right)=\sqrt{\left[A_{0}+m(t)+n_{\mathrm{c}}(t)\right]^{2}+n_{\mathrm{s}}^{2}(t)}
\]
当 SNR 很大时,有下面的近似
\[
E\left(t\right)\approx A_{0}+m\left(t\right)+n_{\mathrm{c}}\left(t\right)
\]
\[
\begin{array}{c}{\therefore S_{o}=\overline{{m_{o}^{2}\left(t\right)}}=\overline{{m^{2}\left(t\right)}}}\\ {\therefore N_{o}=\overline{{n_{c}^{2}\left(t\right)}}=\overline{{N_{\mathrm{i}}}}}\end{array}
\]
得增益
\[
G_{\mathrm{AM}}=\frac{2\overline{{m^{2}(t)}}}{A_{0}^{2}+\overline{{m^{2}(t)}}}
\]
满调幅时,增益也只有 \(\frac{2}{3}\) m(t)最大为 A,则均方值为 \(\frac{A_{0}^{2}}{2}\)
说明其抗噪声性能一般
当采用相干解调时,增益就固定为上式而不受 SNR 影响
当 SNR 很小时
\[
E\left(t\right)=R\left(t\right)+\left[A+m\left(t\right)\right]\cos\theta\left(t\right)
\]
\[
R\left(t\right)=\sqrt{n_{c}^{2}\left(t\right)+n_{s}^{2}\left(t\right)}\quad\theta\left(t\right)=\arctan\frac{n_{s}\left(t\right)}{n_{c}\left(t\right)}
\]
看不懂叭,看懂就有鬼了
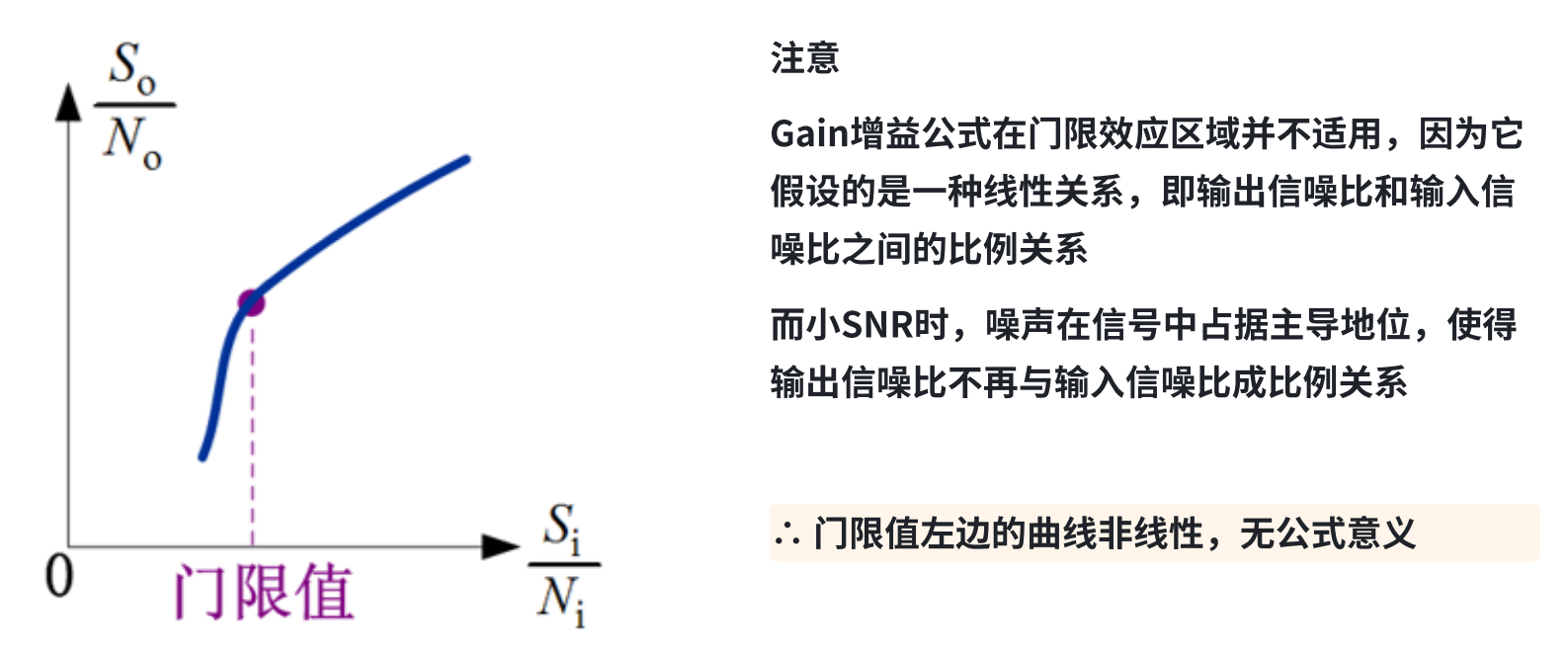
容易得到,信号被噪声所湮没以致完全不可用。这一现象称为门限效应
输出 SNR 开始急剧恶化的结点称为门限值
小结