角度调制¶

约 748 个字预计阅读时间 4 分钟

有关概念与推导下面都不再赘述，只做总结与补充

具体公式推导看这里：通信原理实验折腾 log

概念理解¶

FM 定义式

\[ s_{F M}(t)=A c o s(\omega_{c}t+K_{f}\int_{0}^{t}m(\tau)d\tau) \]

PM 定义式

\[ s_{\mathrm{PM}}(t)=A\cos[\omega_{c}t+K_{p}m(t)] \]

Kp(rad/V)为相偏常数

PM 与 FM 的关系¶

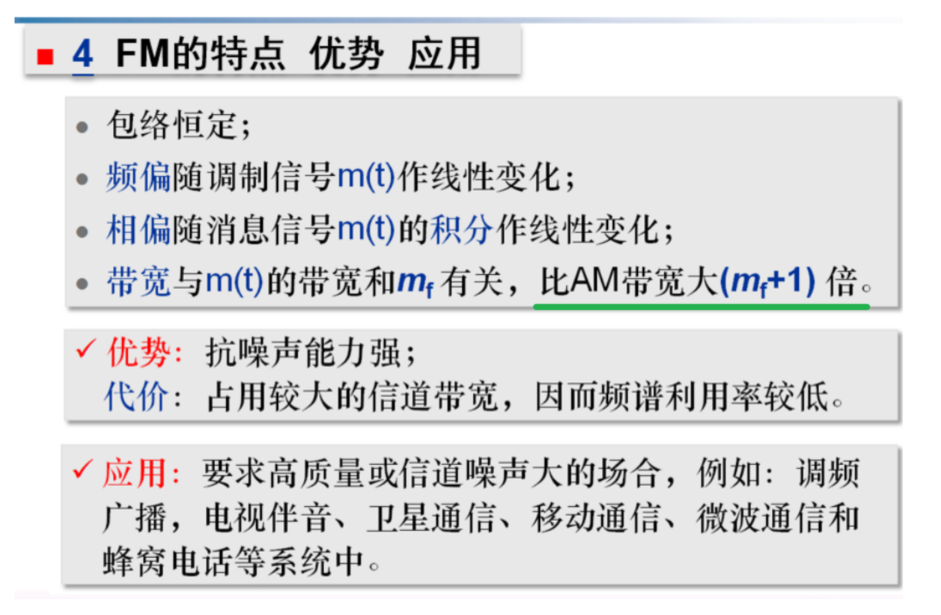
带宽¶

宽/窄带区分、调频指数推导 \(\rightarrow\) 看这里通信原理实验折腾 log

\[ m_{f}\;=\;\frac{K_{f}A_{m}}{\omega_{m}}\;=\;\frac{\Delta\omega}{\omega_{m}}\;=\;\frac{\Delta f}{f_{m}} \]

与传输带宽、功率分配与抗噪性能有关

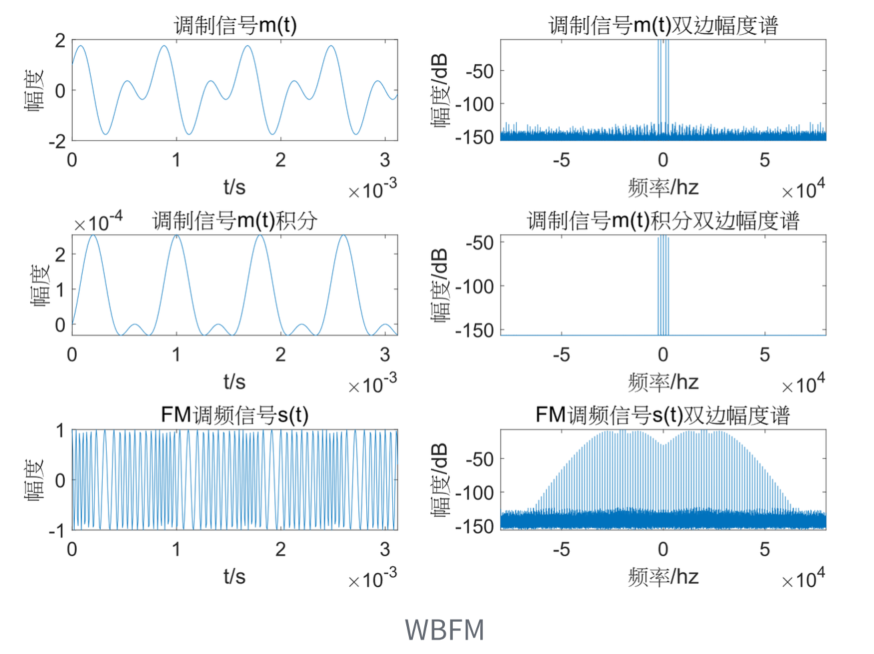
频谱¶

\[ s_{W B F M}(\omega)=\pi A\sum_{n=-\infty}^{\infty}J_{n}(m_{f})\left[\delta(\omega-\omega_{c}-n\omega_{m})+\delta(\omega+\omega_{c}+n\omega_{m})\right] \]

可见，WBFM 的频谱由载波分量和无数边频组成，且不再是调频信号频谱的线性搬移，而是以一种非线性过程

带宽近似¶

用卡森公式计算调频信号的带宽。对于单音调频信号，可得：

\[ B_{F M}=2(m_{f}+1)f_{m}=2(\Delta f+f_{m}) \]

基于公式和经验推得，对于窄带调频，带宽可近似估计为 2fm ，而与最大频偏无关；对于宽带调频，则可近似估计为 \(2\Delta f\)

多音频 \(f_{m}\) 为最高频

功率分配¶

贝塞尔函数控制，调制前后总功率不变而重新分配，与 mf 有关

\[ P_{\mathrm{FM}}=\overline{{s_{\mathrm{FM}}{}^{2}\left(t\right)}}\,=\frac{A^{2}}{2}{{\boxed{\sum_{m=-\infty}^{\infty}J_{n}^{2}\left(m_{f}\right)}}}=\frac{A^{2}}{2}=P_{c} \]

FM 调制方法¶

分为直接与间接俩种，具体见通信原理实验折腾 log

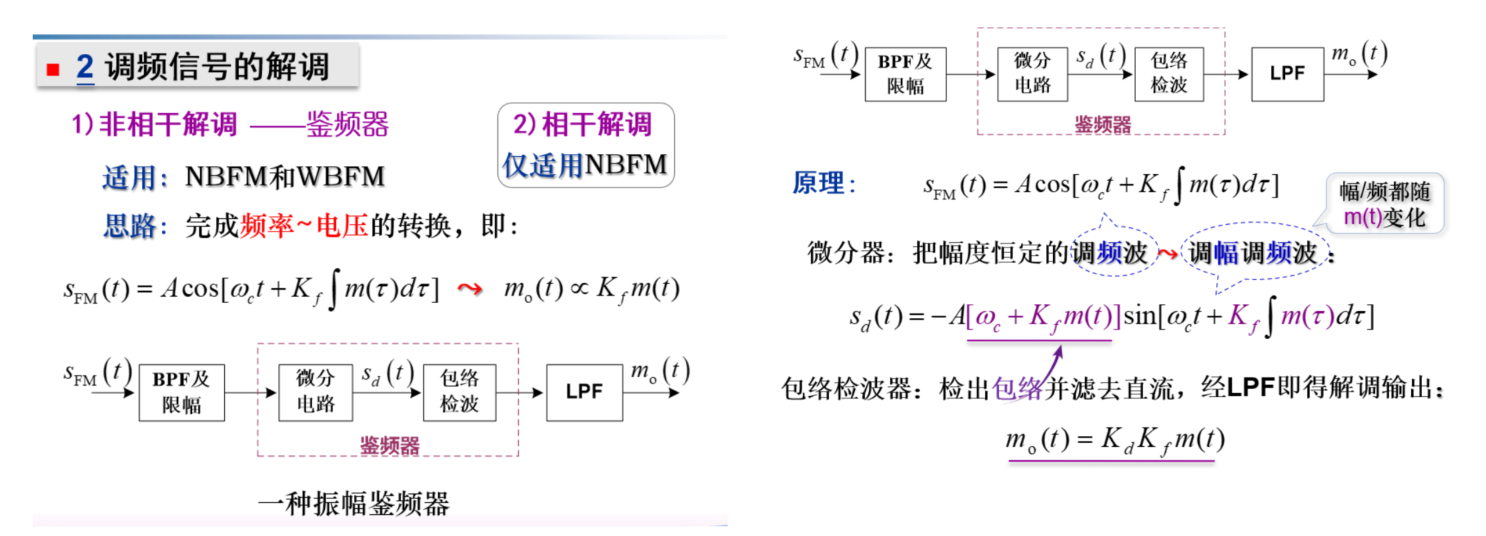
FM 解调方法¶

原理具体解释见通信原理实验折腾 log

课程中重点介绍基于鉴频器的非相干解调

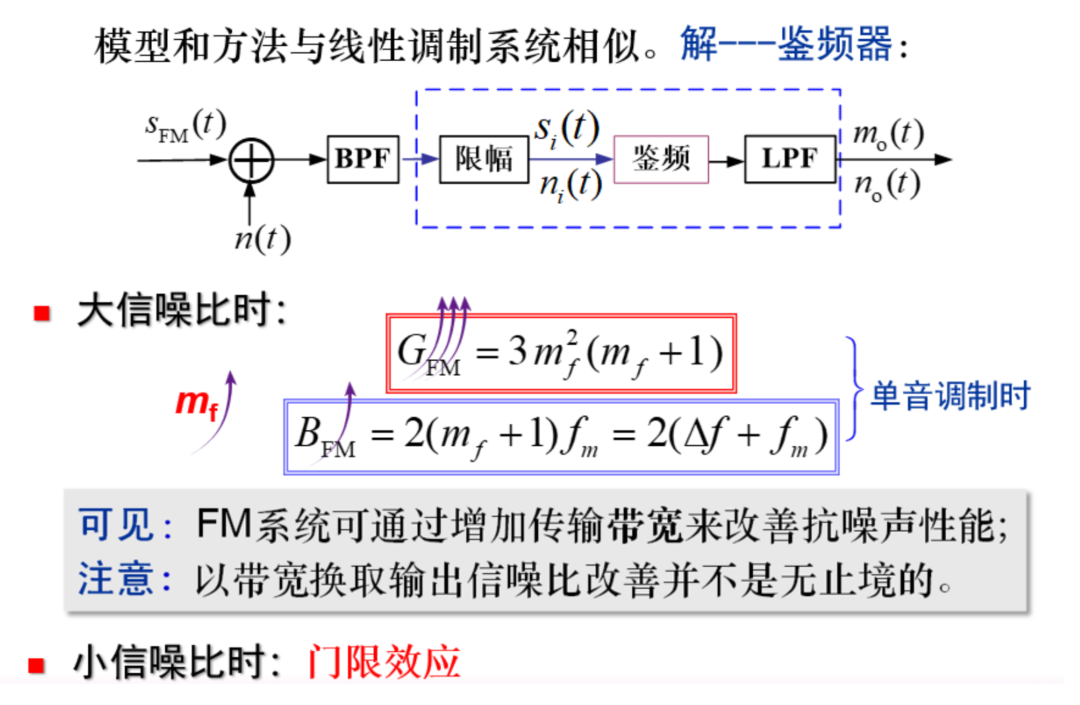
FM 的抗噪声性能¶

用带宽换 Gain

因鉴频器的非线性特征，小 SNR 时也会出现门限效应

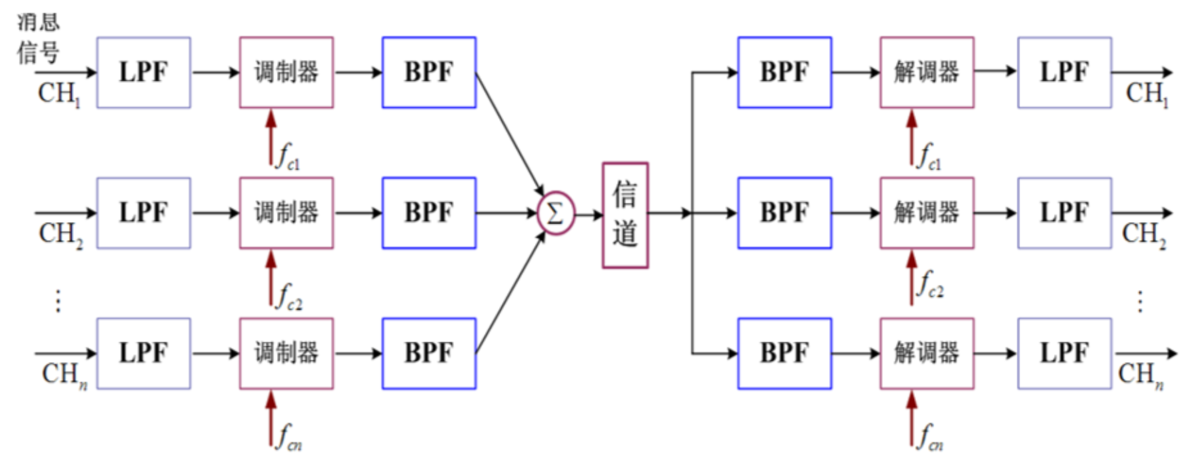
频分复用¶

思考：FDM、FDMA 和 FDD 的区别是什么？

例

已知 \(s_{F M}(t)=100c o s(2\pi\cdot10^{6}t+5s i n4000\pi t)\) ，求

载频 \(f_{c}\)
基频 \(f_{m}\)
最大频偏 \(\Delta f\)
调频指数 \(m_{f}\)

不难得到 \(s_{F M}(t)=A c o s(\omega_{c}t+m_{f}\sin\omega_{m}t)\)

所以 \(f_{c}=1M H z,f_{m}=2k H z,\Delta f=f_{m}\cdot m_{f}=10k H z,m_{f}=5\)

例 | 让 LLM 全军覆没的俩道题

需注意

解调器输出端的信号已经搬回零频，重新考虑带宽，不含负频

SSB 的中频与载频不相等

各个调制方式的比较¶

前提

\(\left.\left\{\begin{array}{l}\text{解调器输入信号功率为 }\mathbf{S_i}\\\text{信道噪声均值为}\mathbf{0}\text{,单边功率谱密度为 }\mathbf{n_0}\\\text{基带信号带宽为 }\mathbf{f_m}\\\text{其中AM的调幅度为 }\mathbf{100\%}\text{,正弦型调制信号}\end{array}\right.\right.\)

必须掌握的