数字基带传输¶
约 3966 个字 预计阅读时间 22 分钟
直接传输基带信号,不含调制解调
这一章重点在基带信号、码型、ISI、频带利用率、滚降系数、抗噪性能分析的概念理解,为数字调制做铺垫
重点
- 六种基本基带信号:单/双极性 归零/非归零码、差分码(绝对码和相对码的概念,编码与译码)、多电平信号。差分编译码是易错点
- 基带信号功率谱密度:连续谱(一定有)+ 离散谱(不一定有)
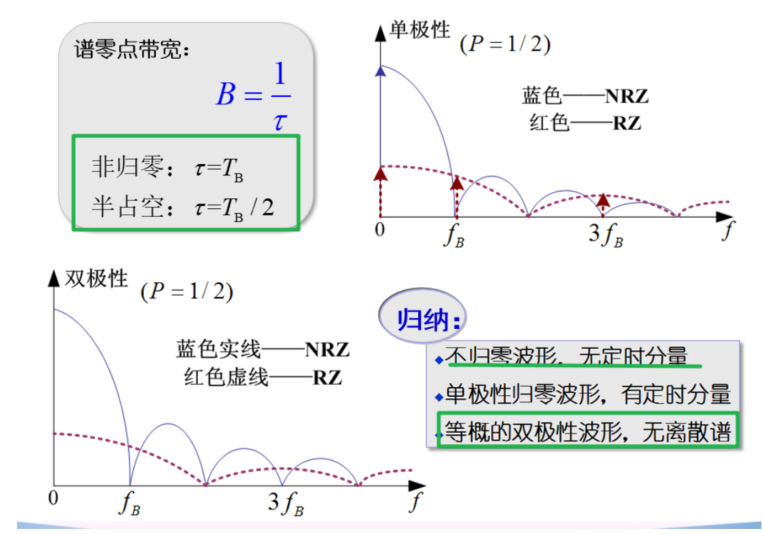
- 能够画出单/双极性 归零/非归零码的功率谱曲线:掌握零点带宽、离散谱位置等
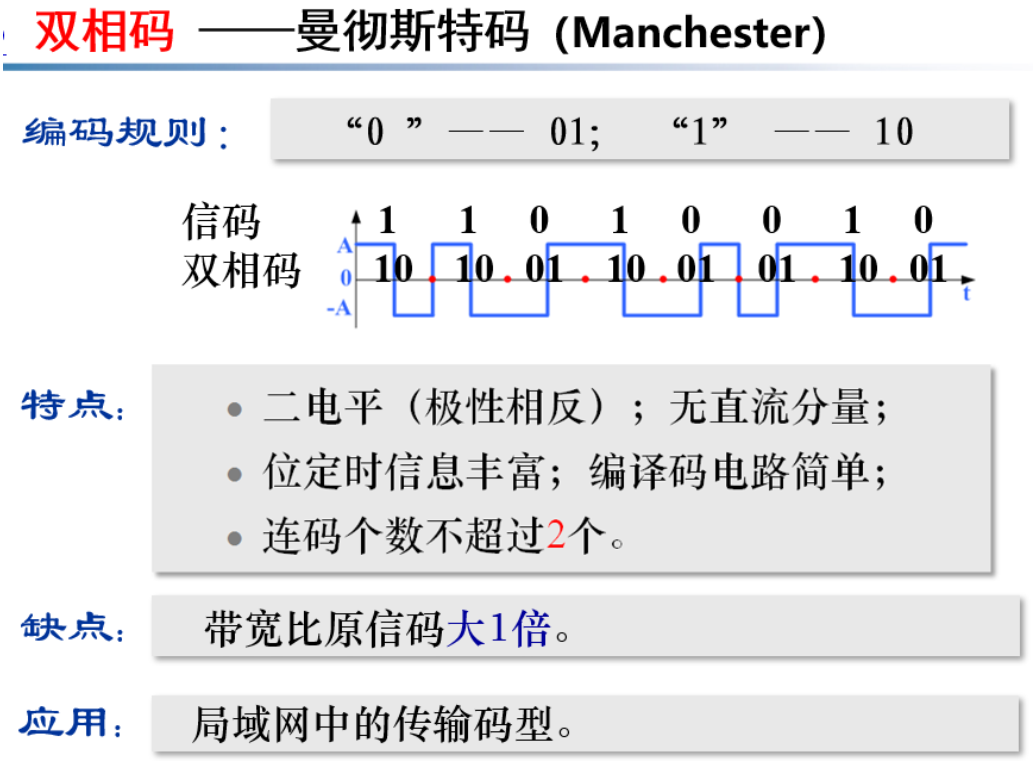
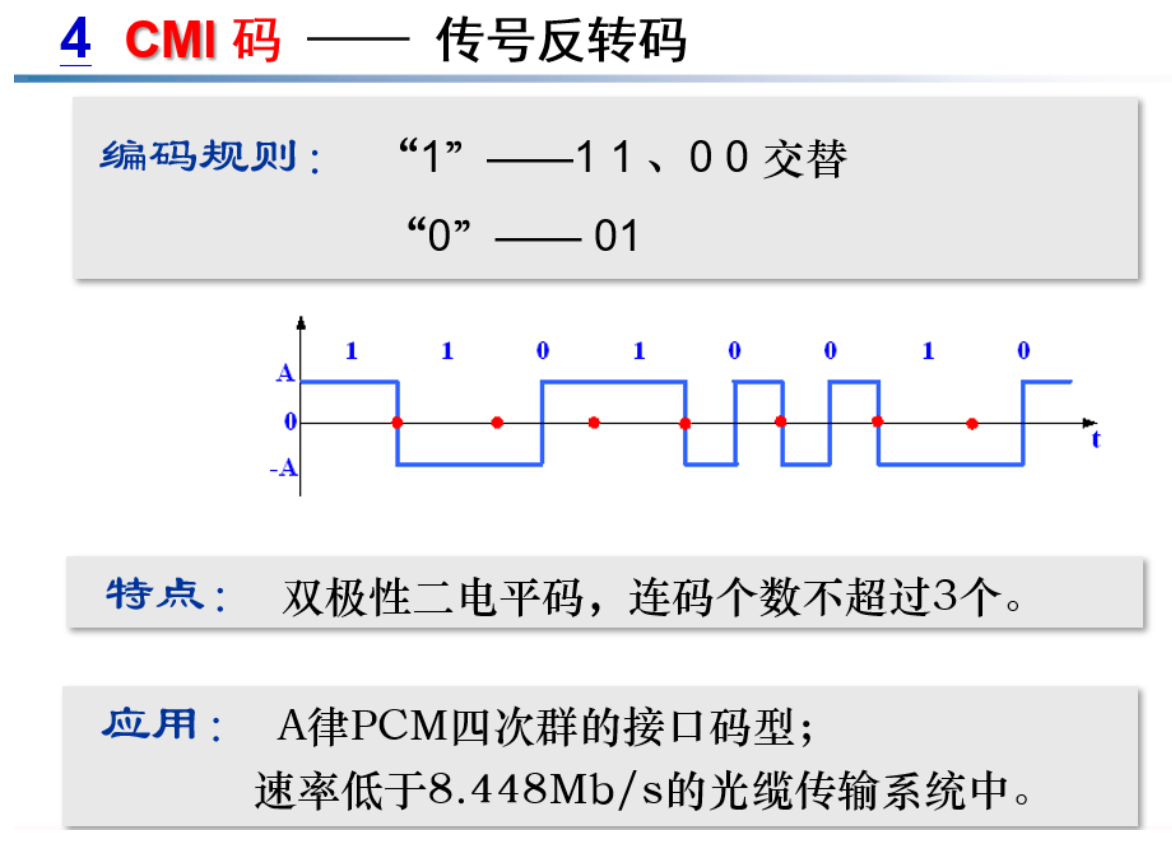
- 几种常用的传输码型(或称为 线路码):AMI、HDB3、双相码、CMI 码、nBmB 码。重点 HDB3 码;概念:许用码组和禁用码组
- 误码的原因:信道噪声、码间串扰,理解产生码间串扰的原因。 眼图。
-
无码间串扰的条件:
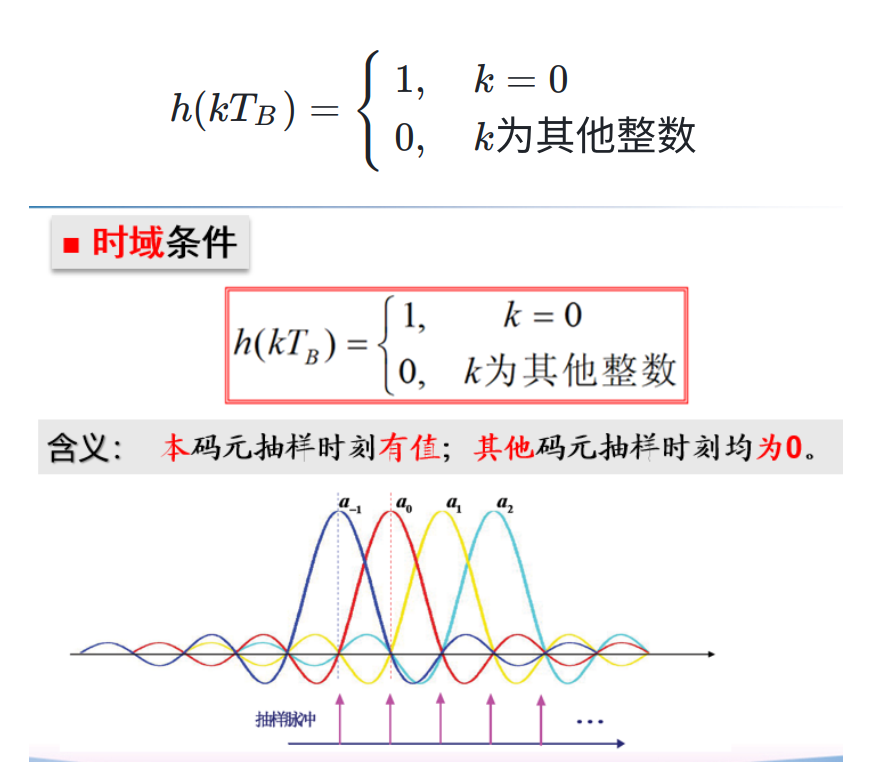
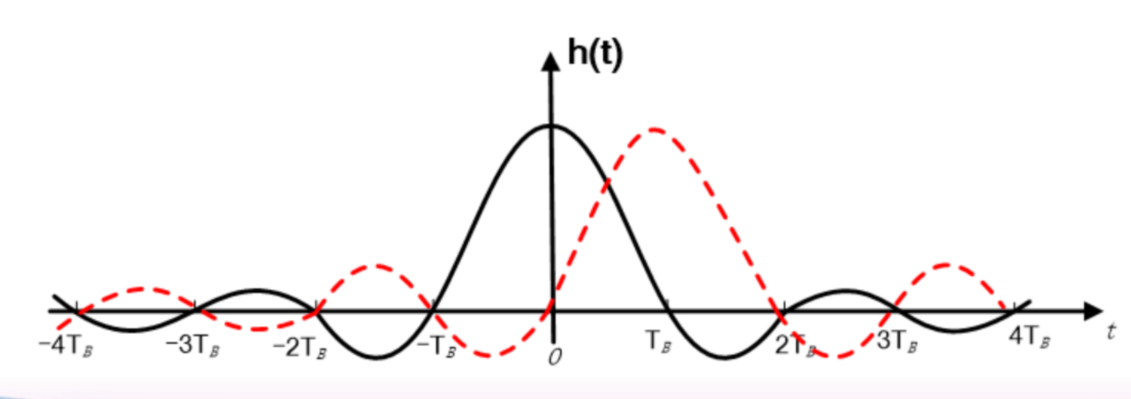
- 时域条件—能够结合 \(h(k T_{B})\) 的图形直观解释
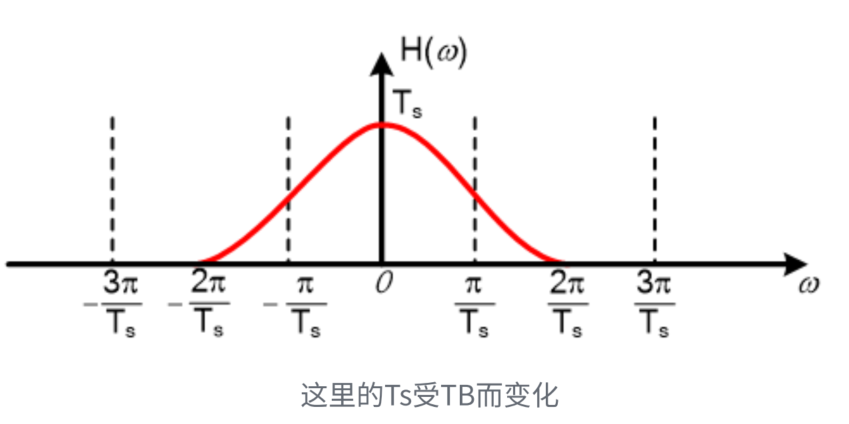
- 频域条件—频域下周期延拓后主值区间表现为矩形
-
余弦滚降特性、奈奎斯特带宽/速率、频带利用率、滚降系数
- 基带传输系统抗噪声性能分析(误码率、最优判决门限)、部分响应系统、时域均值
Why is Baseband Transmission?
近距离广泛使用—数据线
也包含着 ISI、PSD、Pe
带通(含载波)可等效为基带传输系统
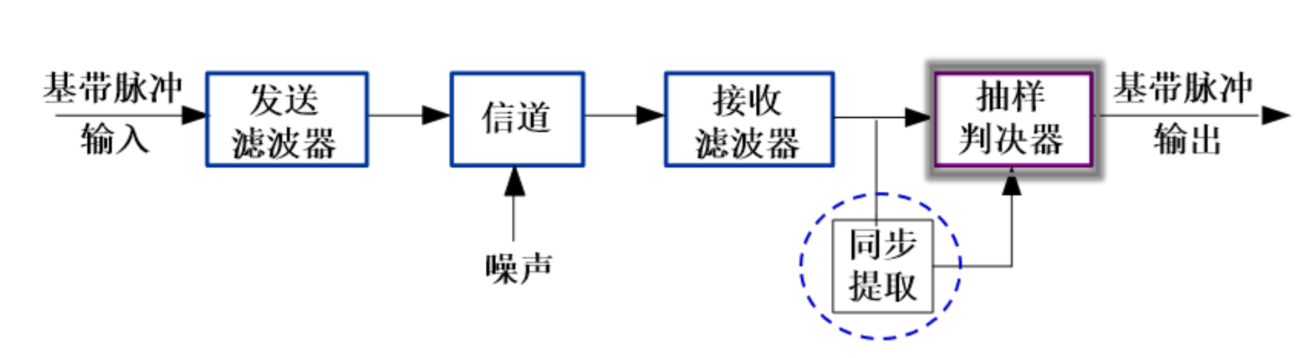
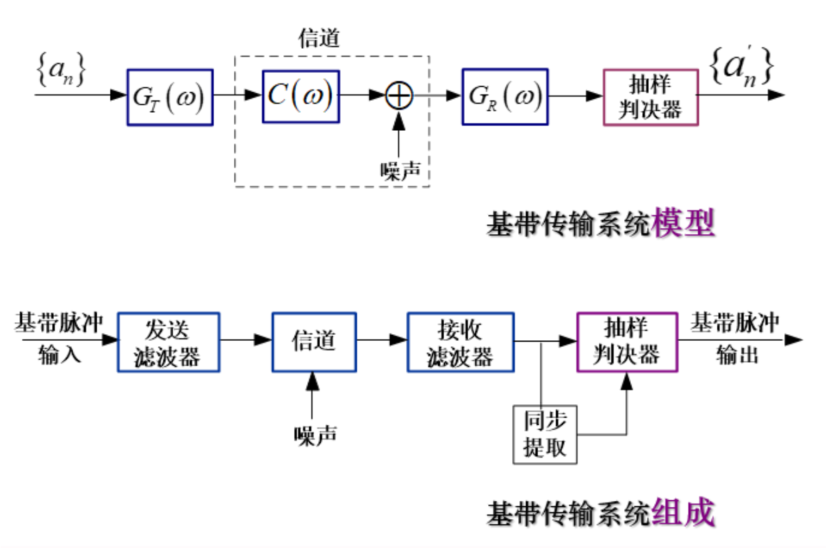
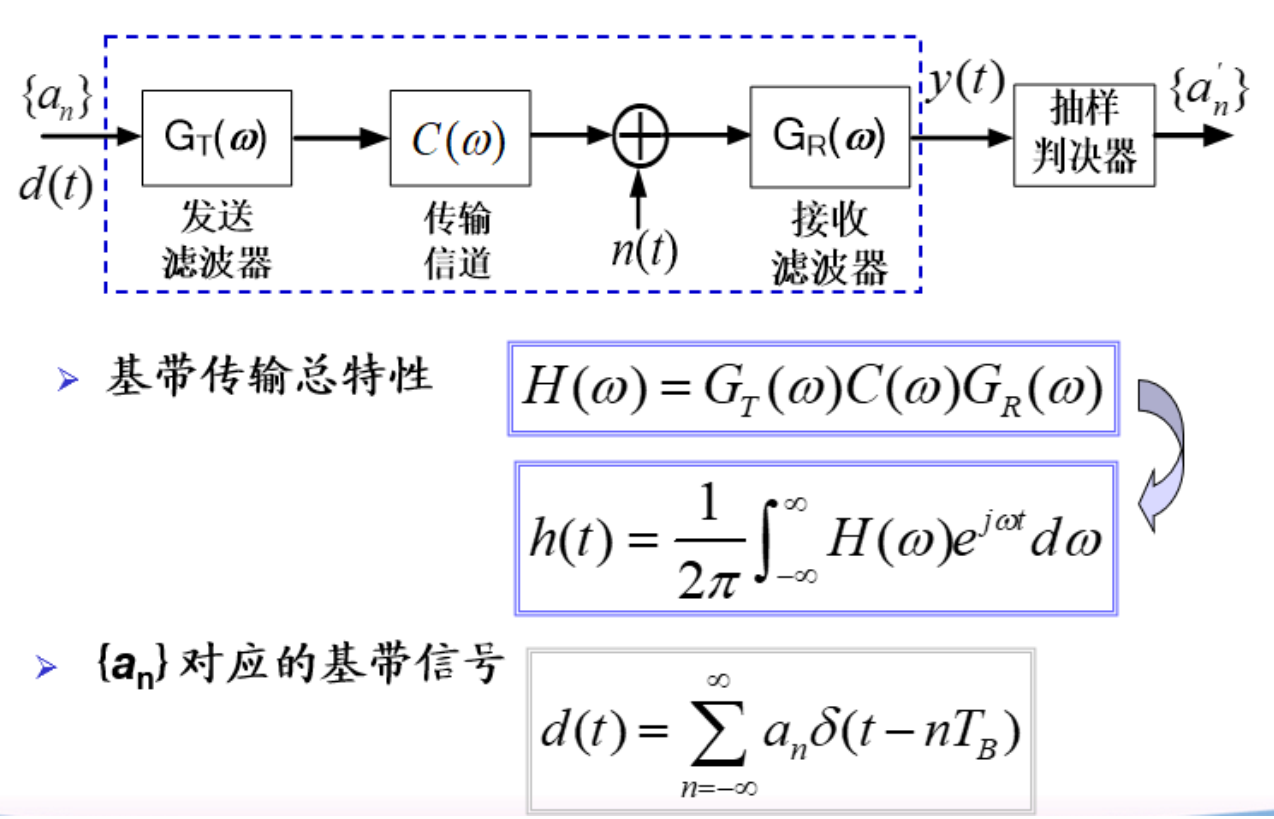
基带传输基本框图¶
包含以下模块:
- 脉冲整形与匹配滤波—发送/滤波器
- 同步—符号定时同步(码元同步)、载波同步
- 抽样判决
数字基带信号特性¶
题外话—时域 | 频域的截断 对 频域 | 时域的影响
- 时域截断,频域主瓣展开,Sa 函数主周期越大
时域截断就相当于增加突变,引生高频分量
- 频域截断,过 LPF,则滤去高频分量,导致信号突变处平滑,滚降时间变长
对于数字信号即码元展宽,易引发 ISI
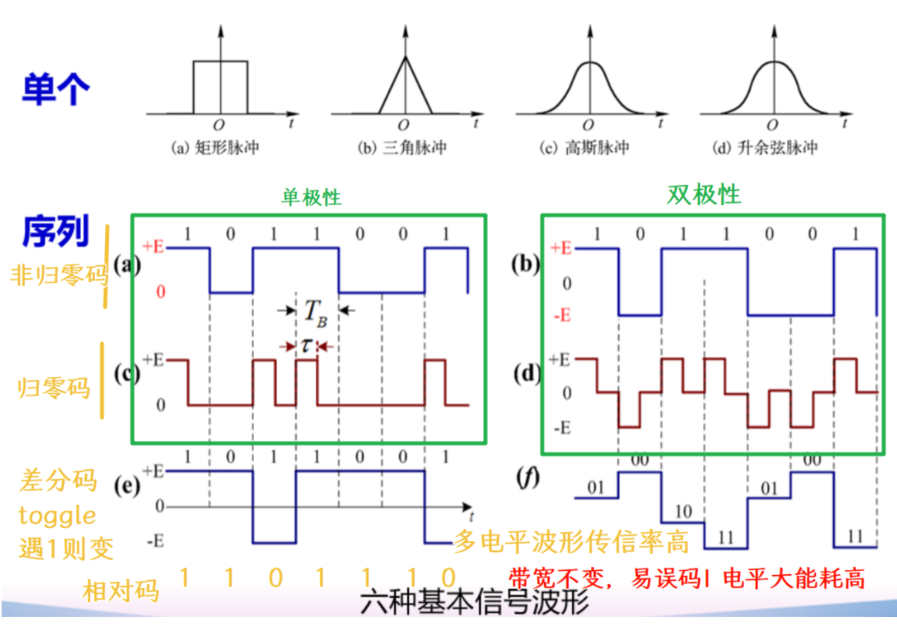
基本信号波形¶
- 归零码(Return-to-Zero,RZ)
存在占空比,可通过冲激信号确定定时分量
- 差分码
一般采用根升余弦滤波器(RRC) 收发各配一个,卷积后即为升余弦(RC)【Acoswt+A/2】
- 多电平波形
数字带宽一般用波特率表示
在此前提下,多电平所占用数字带宽不变,传码率不变下提高了传信率
码元表达式¶
随机脉冲序列表达式
\(a_n\)为电平取值(random)
一般表达式 (二进制下)¶
基带信号的 PSD¶

- 稳态波为统计平均分量,呈周期性
- 交变波为随机表达式
随机脉冲序列为其求和,即
分别求解稳态波与交变波的功率谱密度
- 稳态波在时域周期,则在频域离散,表现为
\(\rm{m=0}\) 对应直流分量;\(\rm{m=1}\) 对应定时分量
- 交变波用定义去解,得连续谱
由表达式可知结论
- 连续谱分量确定零点带宽 B
\(f_{\mathrm{B}}={\frac{1}{T_{\mathrm{B}}}}=R_{\mathrm{B}}\)
由式子决定,这一分量不可能消失(信息一定是不确定非周期的) - 离散谱可在奇数分量确定定时分量(码元速率)
是周期分量,故可能会消失(等概反向,即双极性占空比 \(50\%\) )
常用码型¶
重点是 HDB3
原则¶
- 无直流分量,且低频分量、高频分量小
- 定时信息丰富
- 简单高效
3 阶高密度双极性码(High Density Bipolar of Order 3 code)
目的是解决 AMI长 0 跑飞的问题,但性质上完全不同
加入破坏脉冲 V| 调节脉冲 B,使连 0 不超过四个
规则怪谈
- V 之间极性交替
- V 极性与前一个非零码(包含 V)必须相同,否则用 B 调节【可用于译码时找破坏节 V,相同极性后者 为破坏节】
- V 与之后的正常的传号码极性交替
比如
再比如
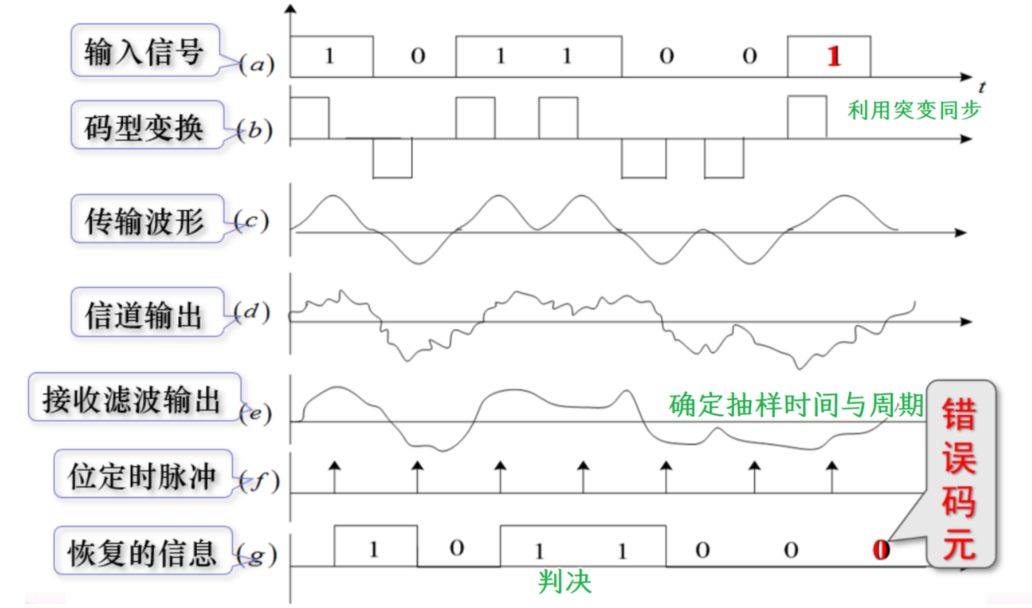
数字基带信号传输与码间串扰¶
产生误码的原因
- 噪声
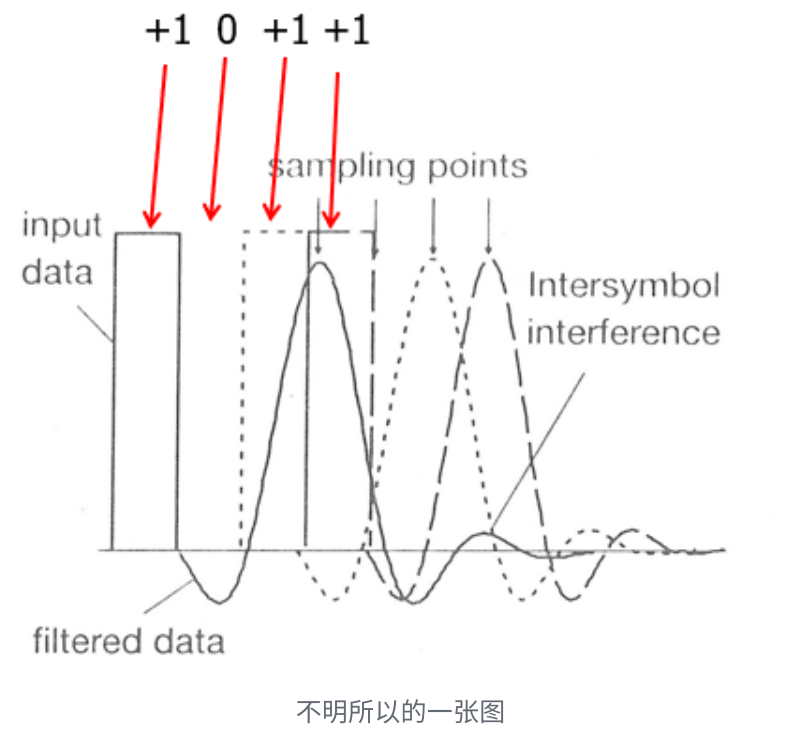
- 信道 LPF 后频域滤去高频,时域展宽,出现码间串扰
码间串扰(ISI)¶
无码间串扰的理想信道(幅频、相频、群延迟)
眼图¶
不再赘述,参见眼图的形成原理
无 ISI 的定量分析¶
接收滤波器输出信号
令抽样时刻 \(t=k T_{B}+t_{0}\) , \(t_{0}\) 为延时。此处暂保留,但不妨令 \(t_{0}=0\)
只关心第 k 个抽样值,则 \({\mathsf{k}}{=}{\mathsf{n}}\) ,有
即希望系统
消除 ISI 的时频域分析¶
通过匹配滤波实现脉冲成型
因为无 ISI,故根据时域特点,有
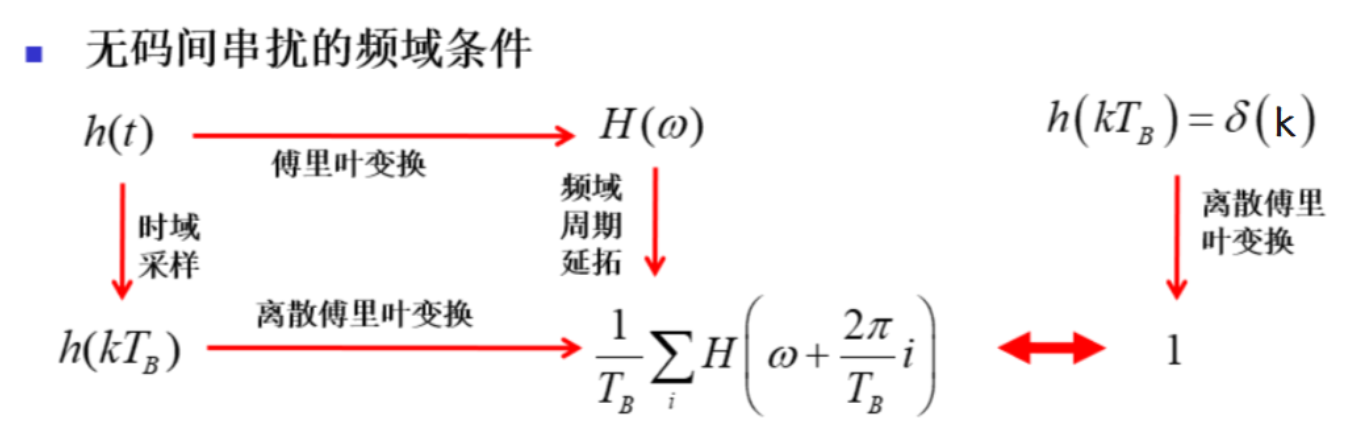
则其 DFT 为 1
时域采样,频域周期延拓,得传递函数表达式
故得到,当冲激函数系数为 1 时,此等式为一常数,即
最后得到频域结论:
一个实际的 H(w)特性若能等效成一个理想(矩形)低通滤波器,则可实现无码间串扰
必考题
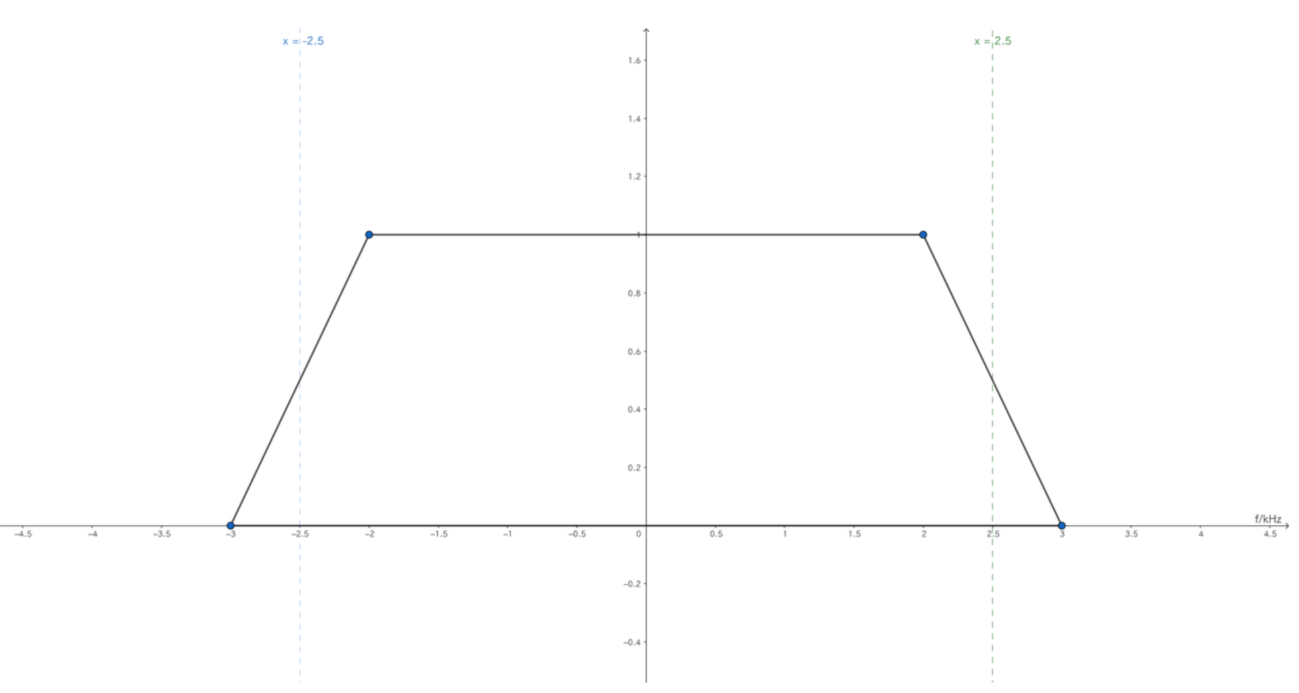
给你一个传递函数的频域波形,再给你传码间隔 \(T_{B}\)
问是否有码间串扰
- 根据 TB 确定 \(\omega_{0}/f_{0}\) ,与传递函数单位相关联(Ts)
- 将传递函数按照 \(\frac{2\pi}{T_{\mathrm{B}}}\) 步长左右延拓
- 取主值区间 \(\left(-{\frac{\pi}{T_{\mathrm{B}}}},{\frac{\pi}{T_{\mathrm{B}}}}\right)\) 相加,观察结果
- 当 \(T_{B}=T_{S}\) 满足条件,则 \(T_{B}=N T_{S}\) 也满足条件(即降传码速率更不会串扰),小数倍则不行
- 无 ISI 最高速率 \(R_{B}=2f_{N}\) (间隔越小越容易串)
滤波器设计¶
理想低通滤波器(奈奎斯特滤波器)¶
奈奎斯特带宽、最高波特率与频带利用率
我们知道了频域表现出理想低通的滤波器不会产生 ISI,于是自然想要进一步压缩带宽
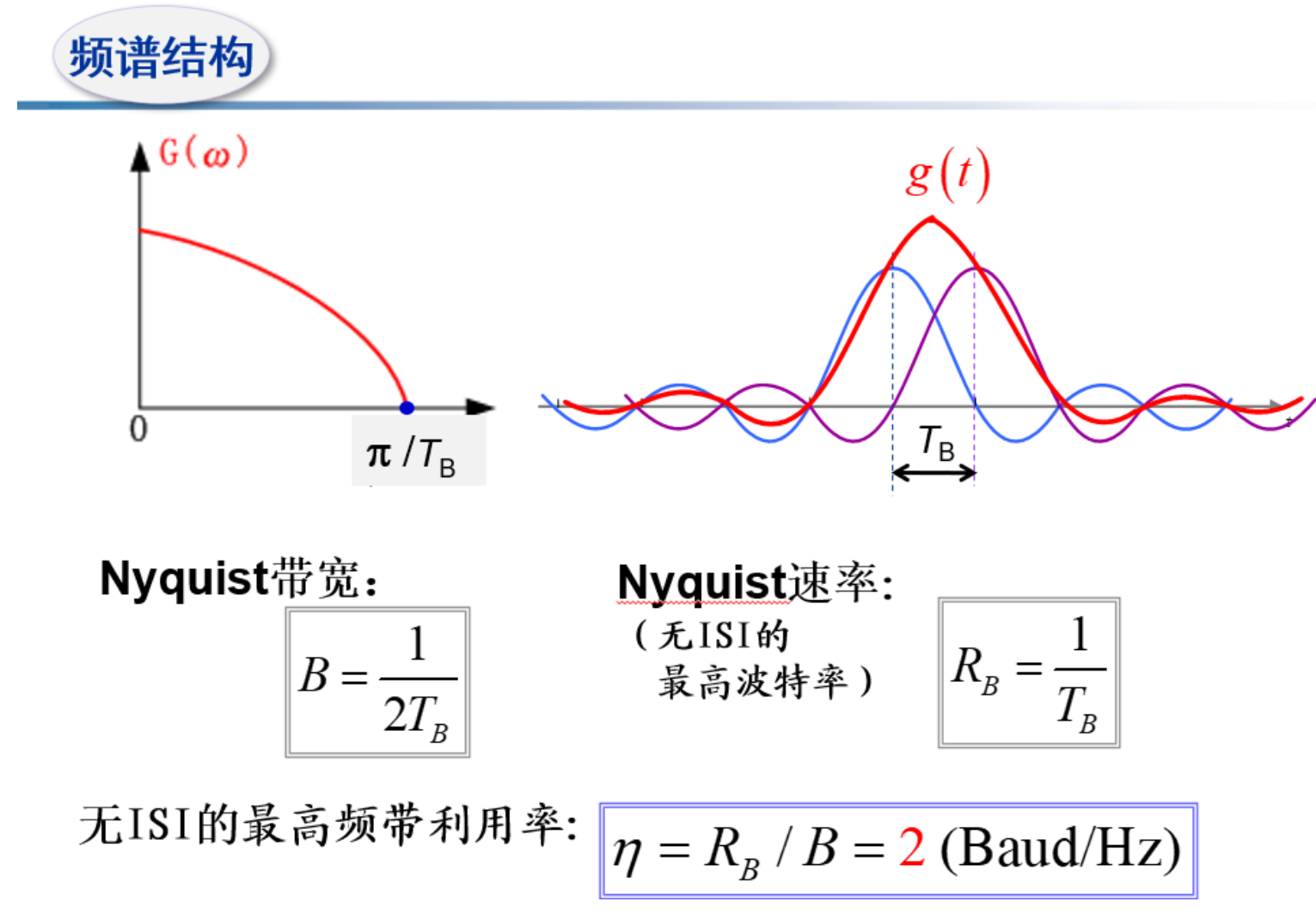
经过上面的【必考题】,我们发现当 \(T_{B}=T_{S}\) 时已是极限,时间间隔不能再短了 此时传递函数频域带宽最为极限,称为奈奎斯特带宽,即
而无 ISI 的最高波特率—奈奎斯特速率为
故最高频带利用率为
频带利用率不会超过此值
转为比特为单位,有
余弦滚降滤波器¶
引入通带与阻带,类似 VSB
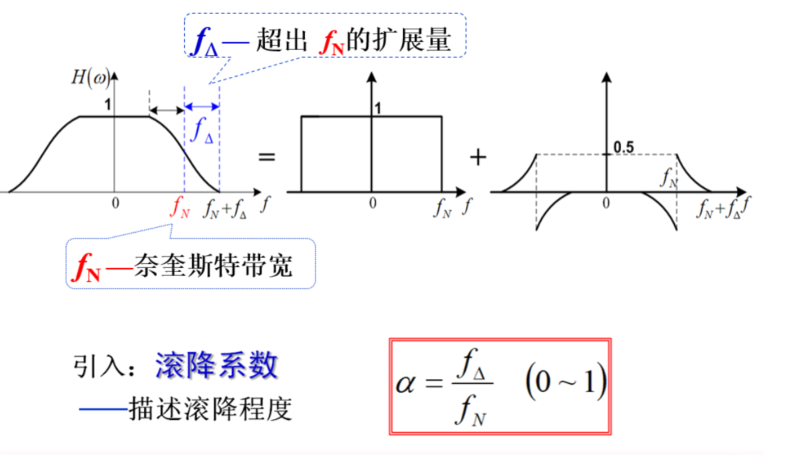
滚降系数
可以理解为以(\(f_{N}\) , 中心)为圆心,把左上角挖了一块到右下角
挖的宽度与 \(f_{N}\) 的比值称为滚降系数
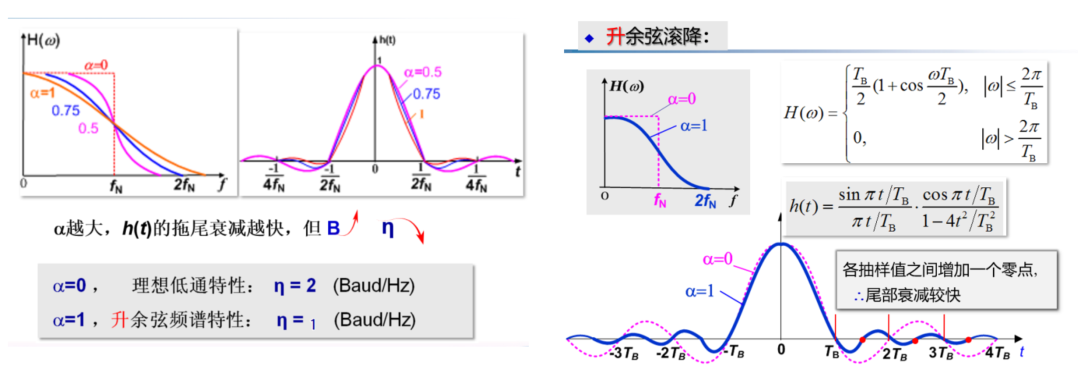
\(\alpha=1\) 时为升余弦,即 1+coswt
注意,最大无 ISI 速率与滚降系数无关,只看 \(f_{N}\)
频带利用率
最终表达式
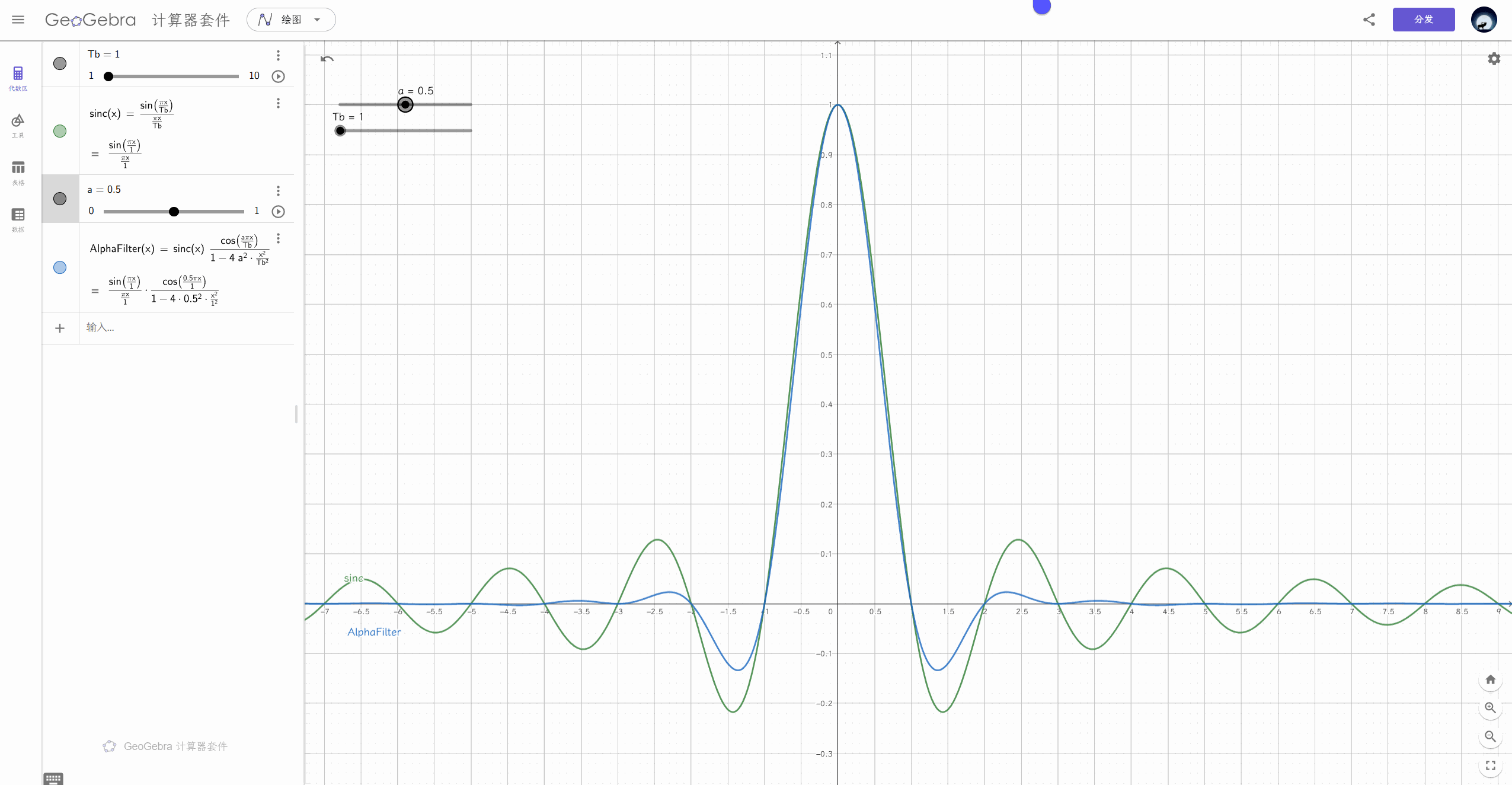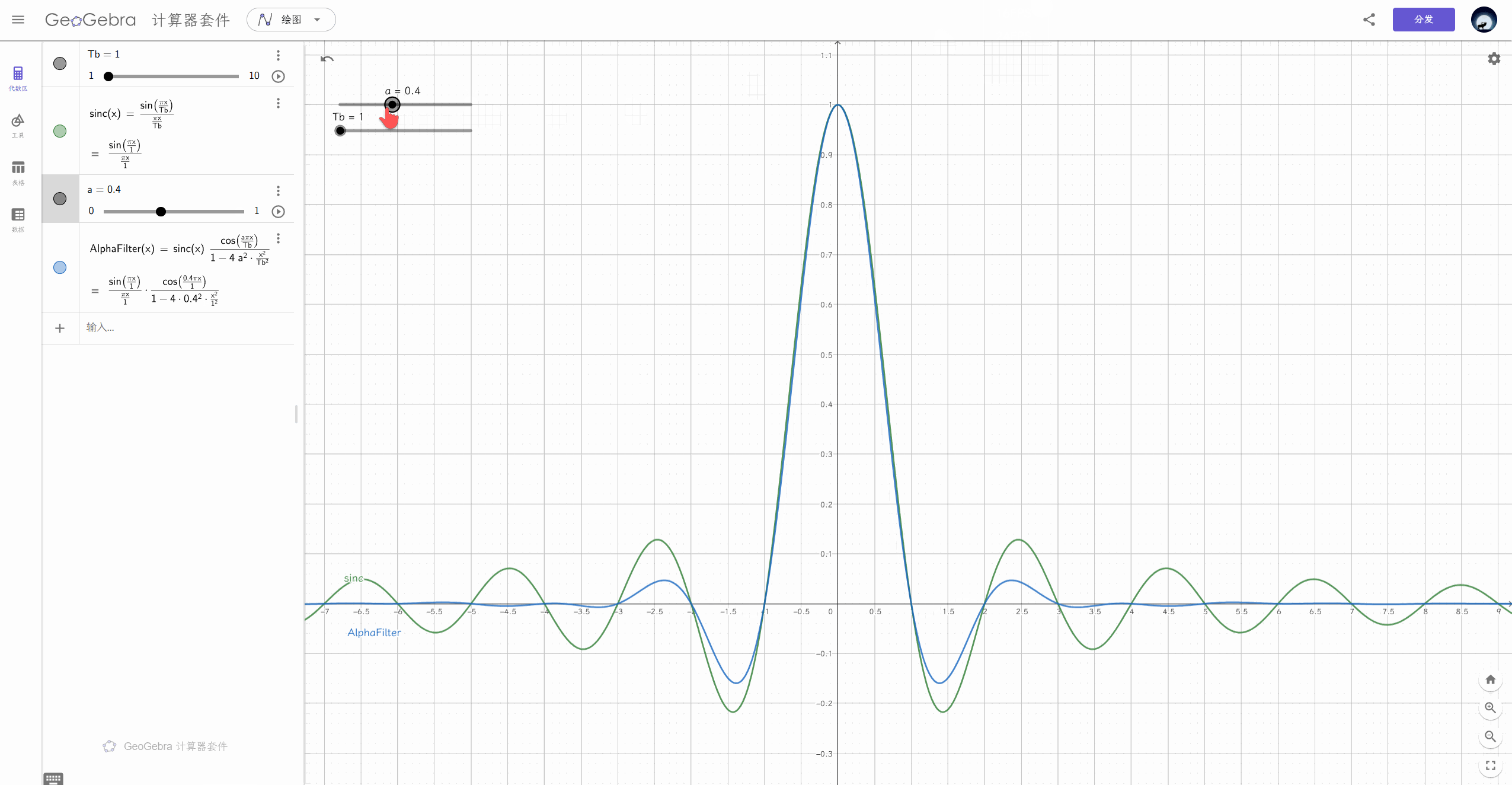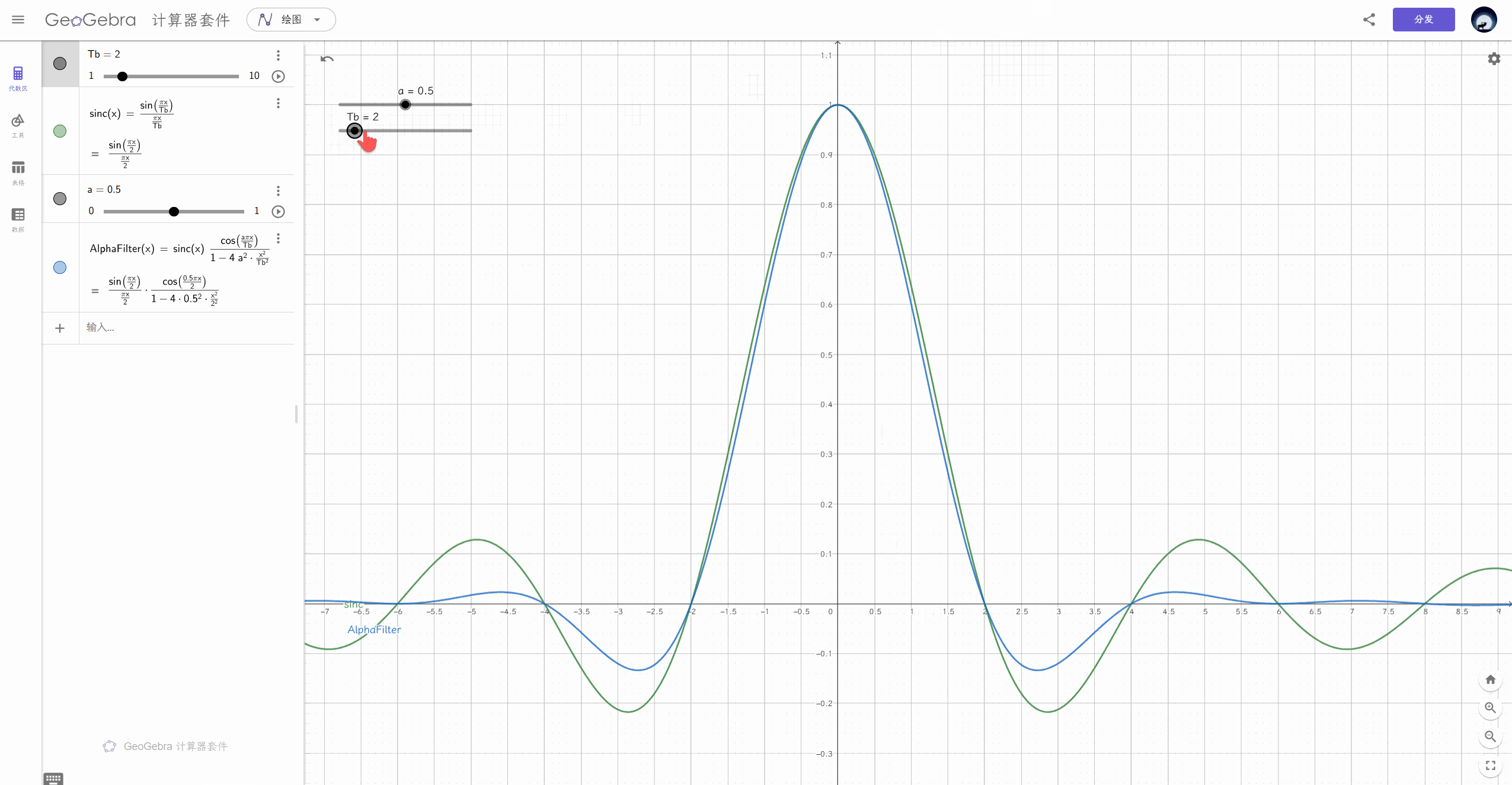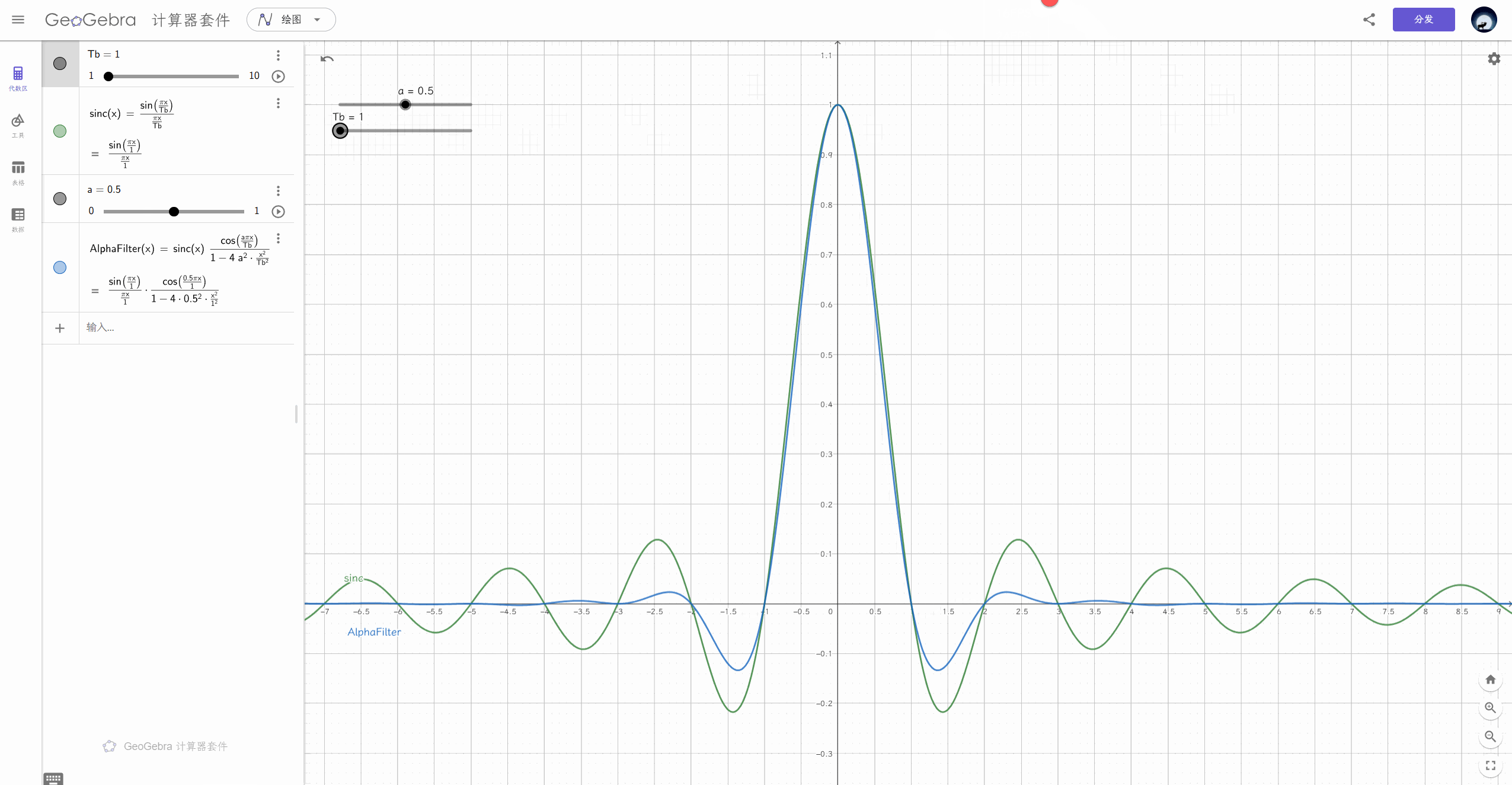
时域上有
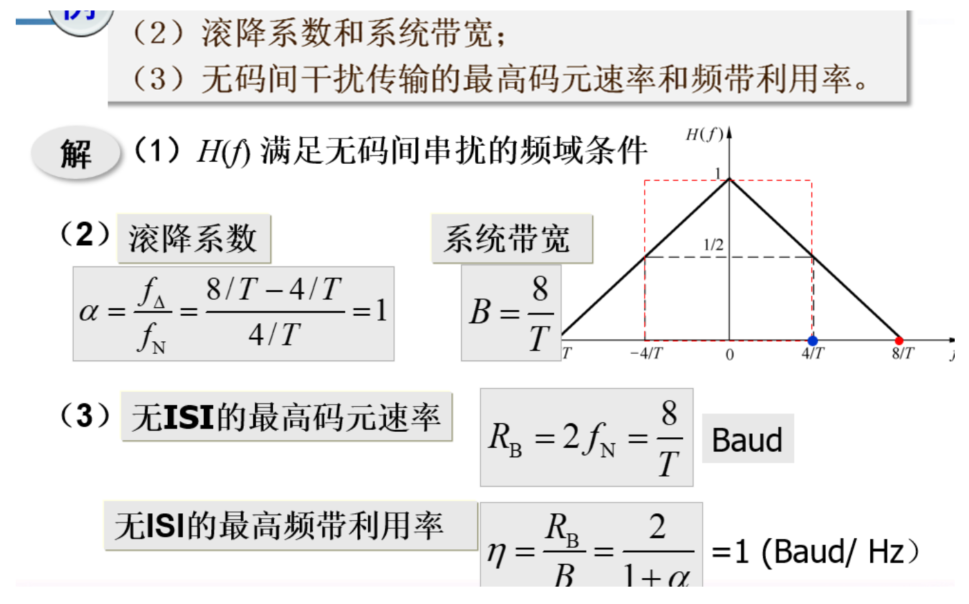
例
有系统函数如下所示,求\(f_N\mathrm{、}R_B\mathrm{、}\eta\)
题外话—能否把俩种滤波器优点 IN ONE 呢?
可采用部分响应技术来同时实现,将在后面说明
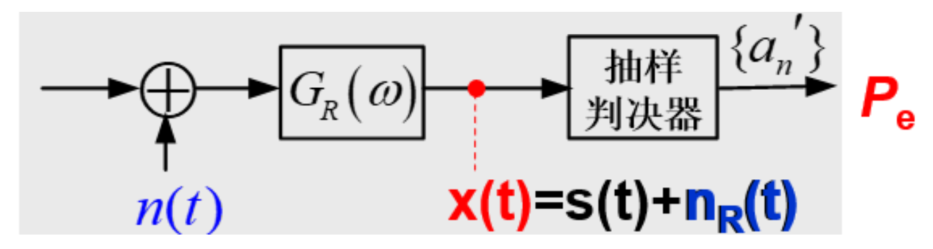
抗噪性能¶
定量分析噪声影响下抽样判决鲁棒性无 ISI 条件下,噪声引起的误码率 \(P_{e}\)频谱
在双边带下分析
二进制双极性基带系统¶
输入高斯白噪声均值和功率谱密度分别为
高斯白噪声经过线性系统仍为高斯,有
均值为 0,故方差即为功率
则得到高斯白噪的概率密度函数
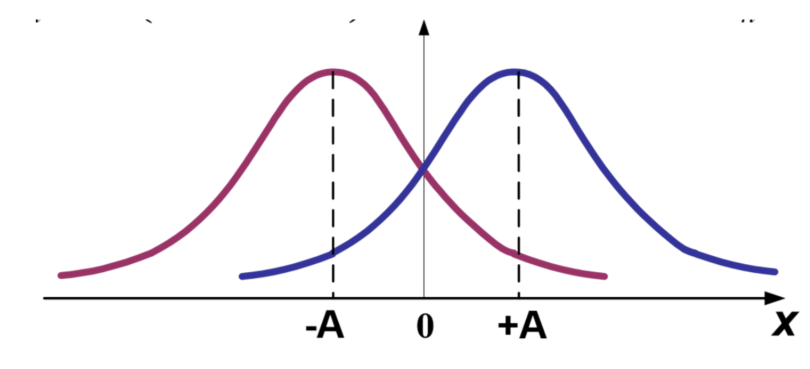
对于双极性抽样判决,这里以高电平为 1,否则为 0
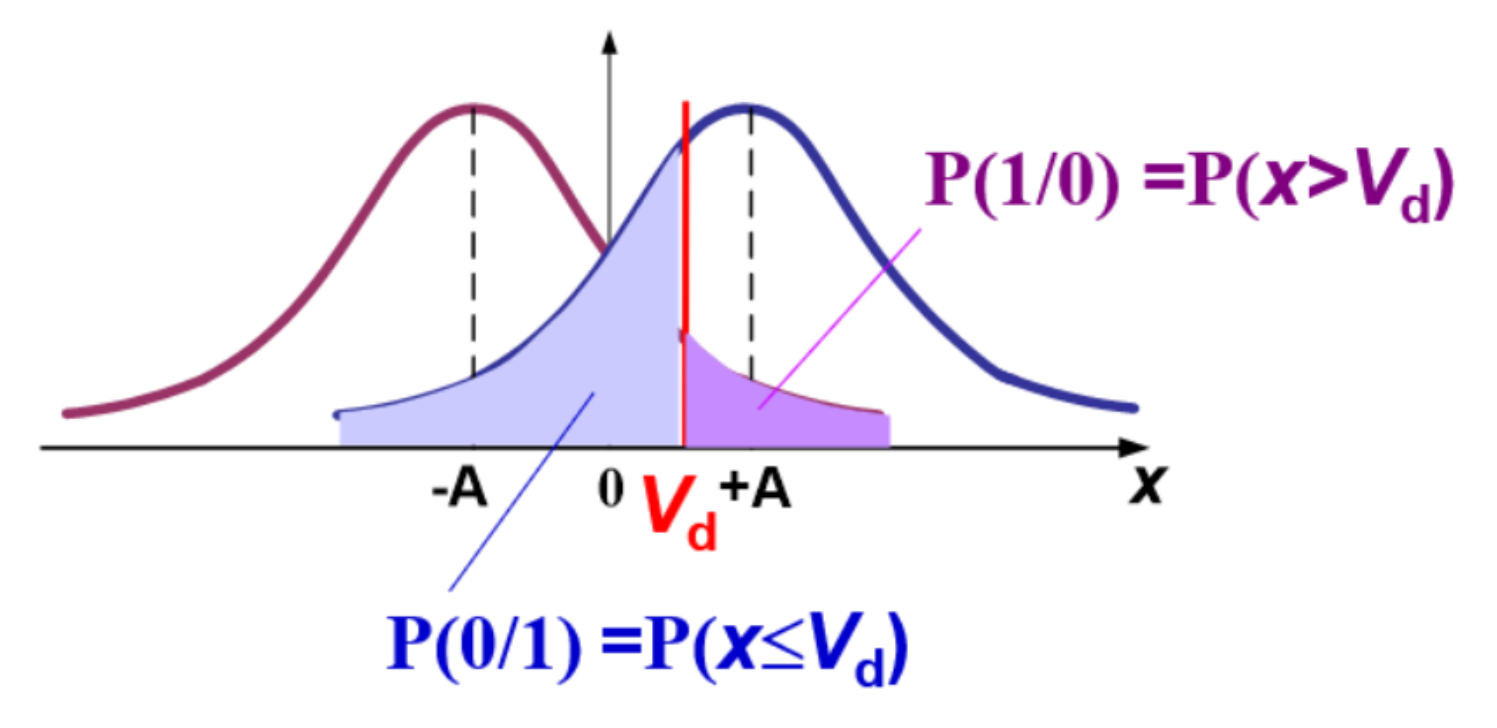
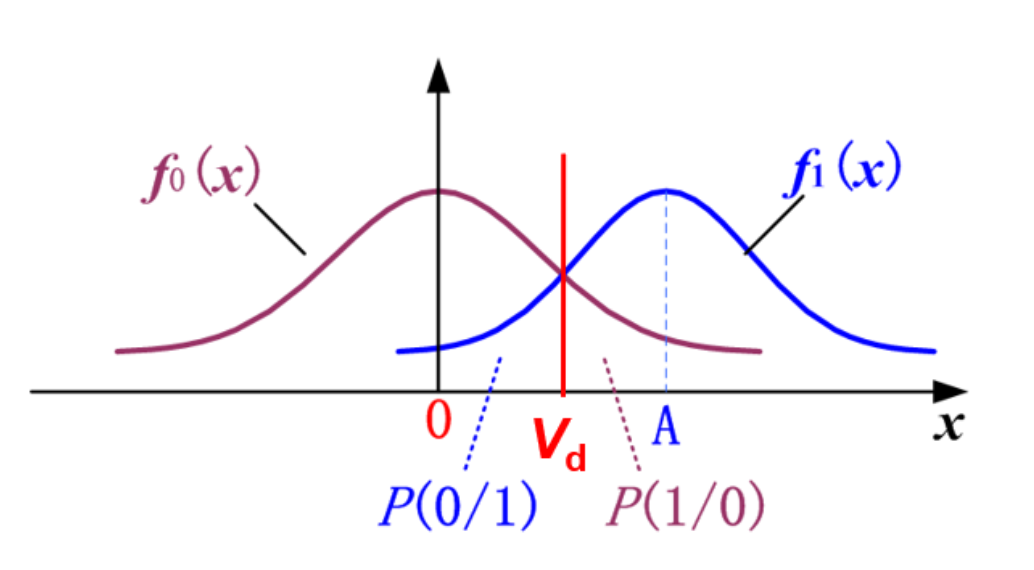
再讨论误码率 \(P_{e}\) ,不难观察为全概公式,即 \(P(\text{发}0\text{判}1)+P(\text{发}1\text{判}0)\)
令门限值(判决电平)为 \(V_{d}\) ,用图像表示为
与概率论中的【上\(\alpha\)点】有些许类似
最后整理得
希望通过下面的解释能让你理解性的记忆这一结论
全概公式自不用多说,关键在于如何记忆/区分两个条件概率 或者说,需要理解 \(e r f(x)\) 是什么东东
误差函数定义上有
这里就有一个【常识】了,即标准高斯变换
再转头看我们的 \(e r f(x)\) ,发现积分限只有一半(偶函数),系数 \({\bf a}{=}{\bf1}\) ,则
非常 amazing 啊,看来误差函数随着输入的变大而趋向于 1
现在再回头, \(\mathrm{erf}(\frac{V_{d}-A}{\sqrt{2}\sigma_{n}})\) 就很好解释了,这一项是发 1 判 0,所以概率密度函数均值在 A
同理可解释为什么另一项是 \(\mathrm{erf}\big(\frac{V_{d}+A}{\sqrt{2}\sigma_{n}}\big)\) ,即标准化
接着我们需要解释如何记忆误判函数前面的正负
根据上面误差函数单调增的性质,再回想我们这个是误判概率哇,即越大说明越容易误判
对发 1 判 0 来说,【门限值越靠近 A(越大),越容易误判】
说明 \(\mathrm{erf}(\frac{V_{d}-A}{\sqrt{2}\sigma_{n}})\) 前面的系数是正的,对吧, \(V_{d}\) 越大误差函数越大,误判概率越大,正相关
反之,得到 \(\mathrm{erf}\big(\frac{V_{d}+A}{\sqrt{2}\sigma_{n}}\big)\) 前系数为负
至于为什么是 \(\frac{1}{2}\) ,我 布吉岛
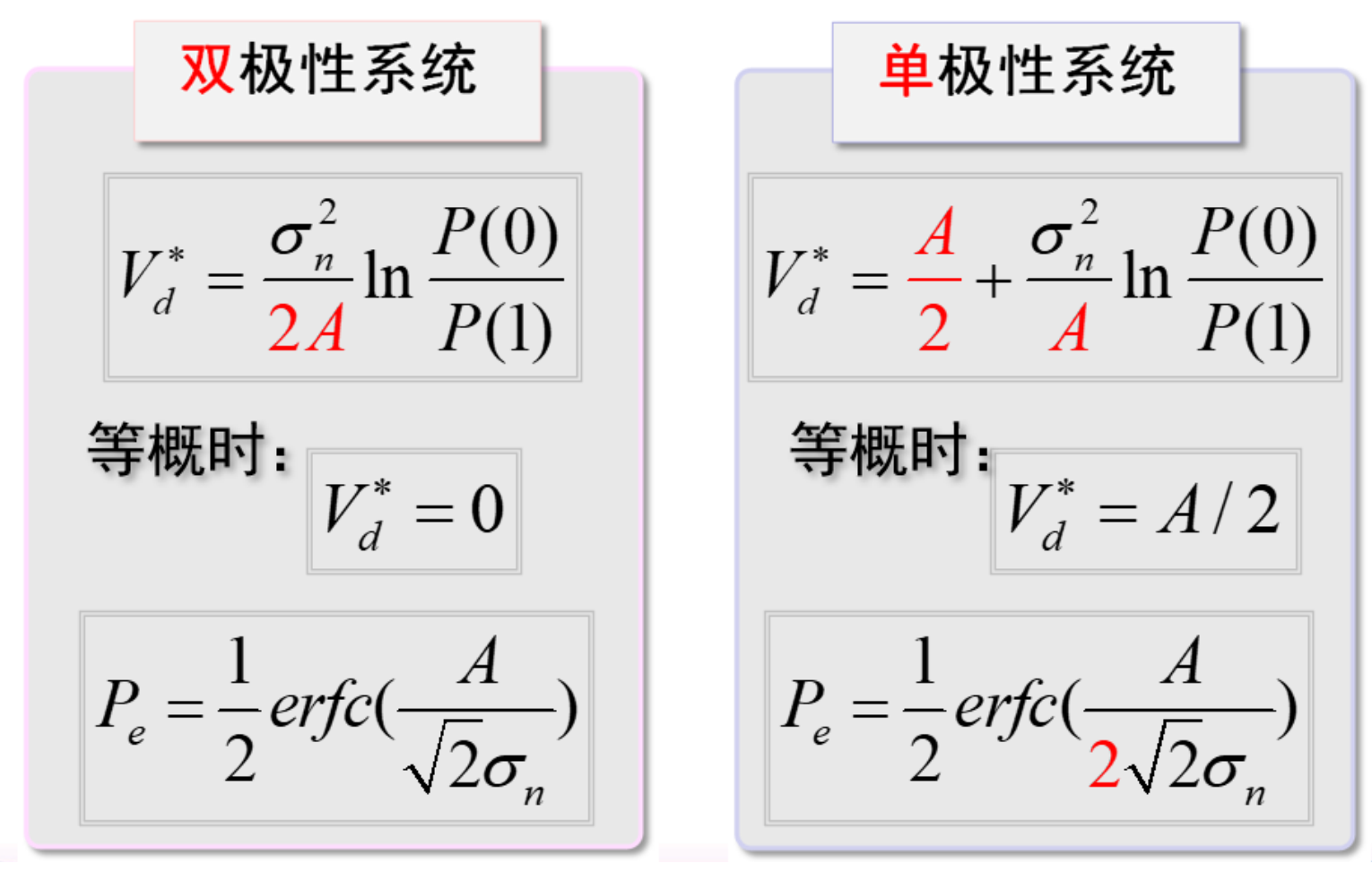
最佳判决门限—使误码率最小
误码率对门限电平求偏导(这是真记不住,考试也会给的)
一般传输时尽可能保证 0/1 信息等概,为了保持最大信息量
此时最佳门限电平为
此时误码率简化为
这一表达式将在下一章再见
二进制单极性基带系统¶
与双极性相比,把其中一个分布移动到 0 即可
部分响应与时域均衡¶
这是改善系统性能的俩种措施
部分响应¶
引入有规律的码间串扰,使之只对后一个码元产生影响(影响可控),类比循环前缀 CP
- 改为三电平,对干扰容忍度下降,但得到更好的判决,且提升频带利用率
- 减少拖尾
- 提升带宽利用率
- 噪声容忍度下降
此处只讨论第一类部分响应
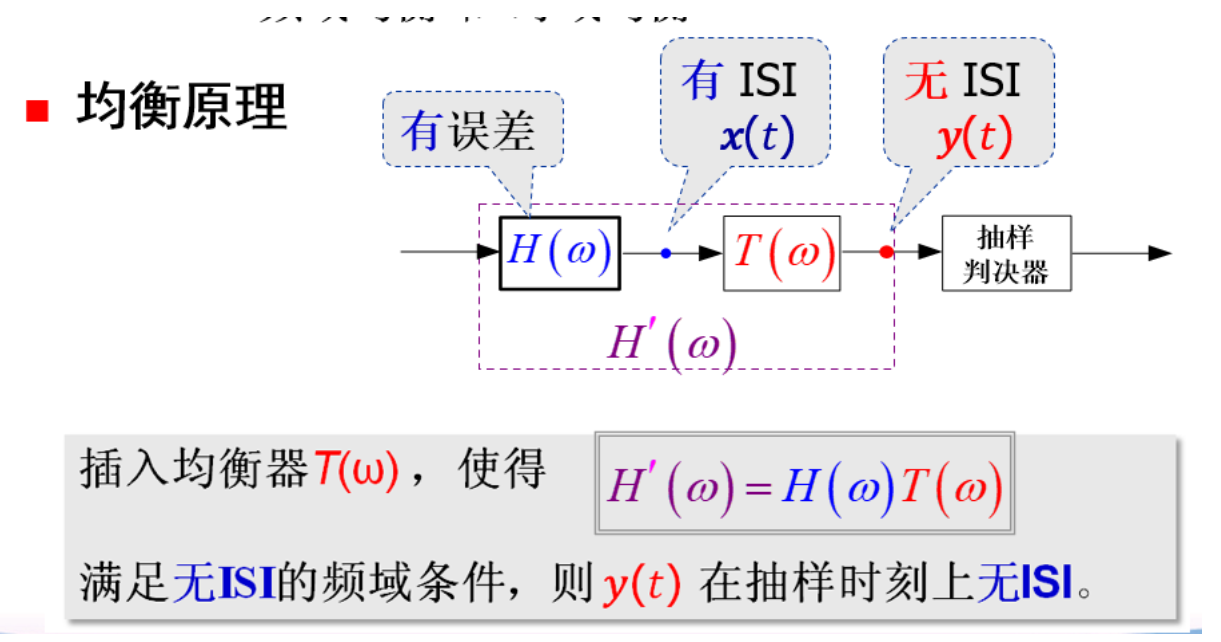
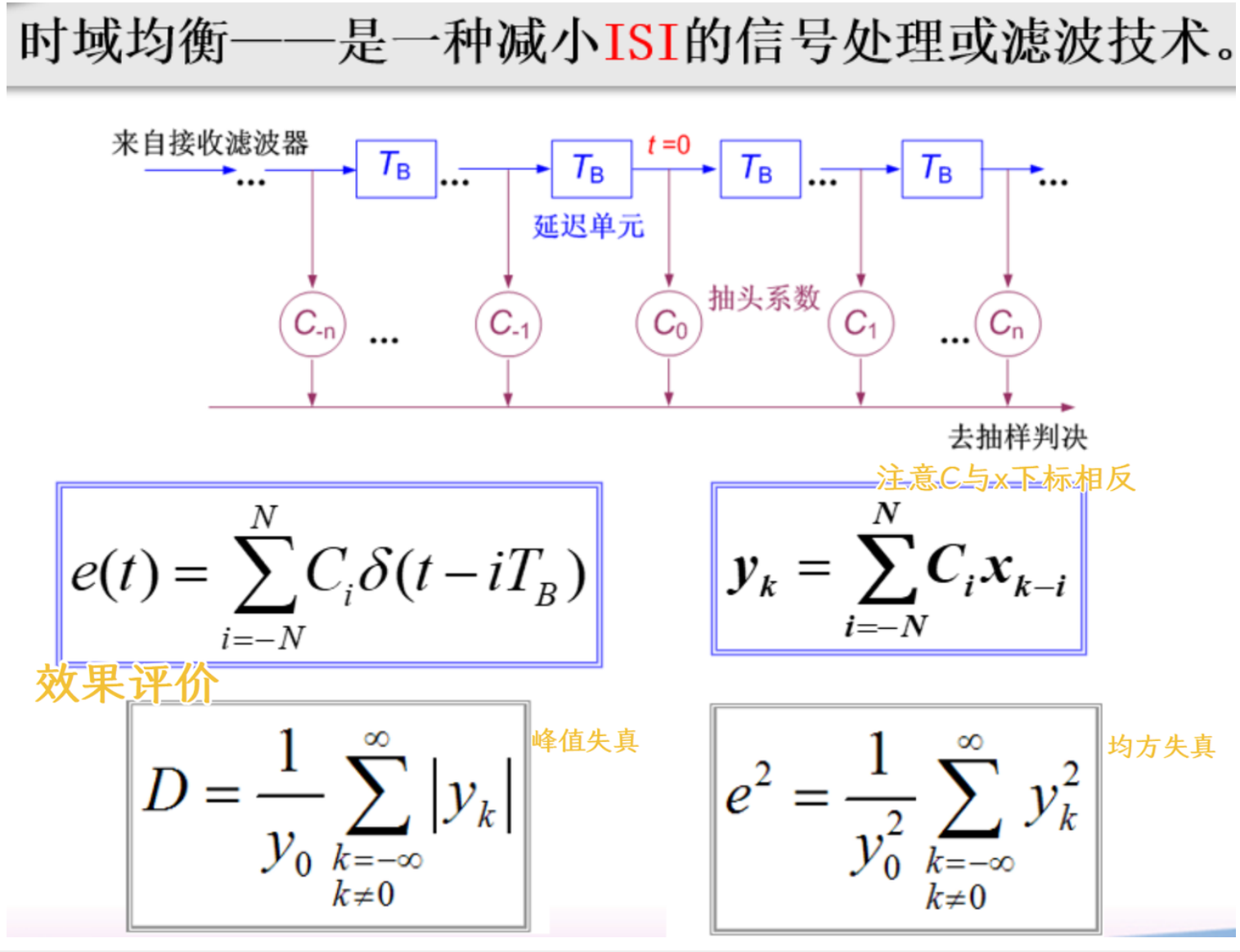
频域均衡与时域均衡¶
通过滤波器补偿以减小 ISI
工程上会传导频做信道估计(求均衡器参数 \(\mathsf{g}(\mathsf{t})\) ),从而使得 \(h(t)*g(t)=\delta(t)\)
时域上通常采用FIR而非 IIR,因为
- 稳定,无反馈,规避自激振荡
- 设计简单线性,相位处理方便