数字带通传输—数字调制
留点印象
- 随 SNR 的增加,QPSK、8PSK、QAM、64QAM,传码速度上限增加
- 距离基站越远,越要考虑抗噪性能(比如远的选 BPSK)
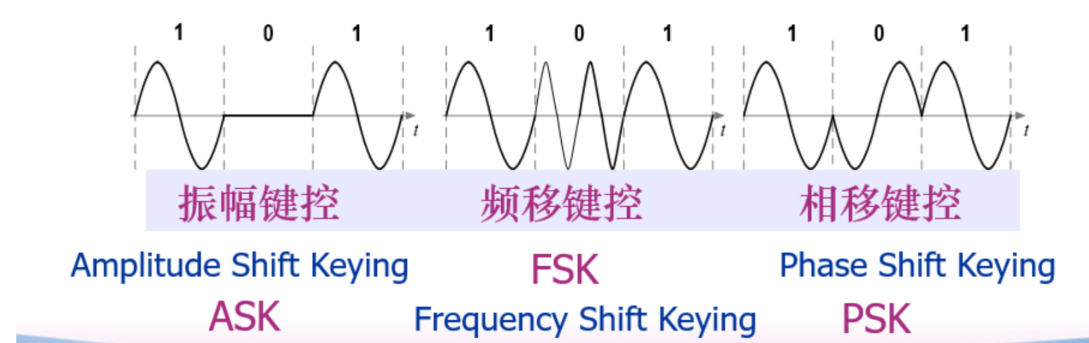
WHAT IS SK?
偏移键控(shift keying),即通过正弦波特征对数字信号编码
基于幅值、频率、相位的载波参数控制,可分为ASK、FSK、PSK
二进制数字调制原理
总体可分为三板斧
写在前面
接下去你可能会看见一个码元宽度含 1 个、2 个、...载波周期
这并不是随便画的
一般会给出码元速率(并不是码率!)和载频 ,即 \(R_{B}\) 和 \(f_{c}\)
例如 \(R_{B}=1K B a u d\) , \(f_{c}=3K H z\) ,则,一个码元宽度里有 3 个周期
以此类推就 OK 啦
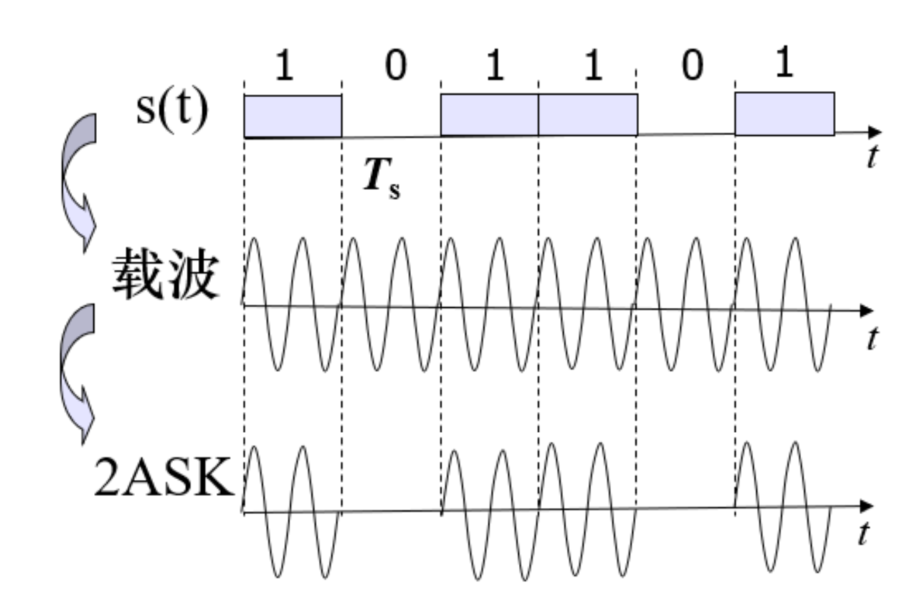
振幅键控 (2ASK)
小名 OOK 为什么没有 OKK
表达式
\[
e_{\mathrm{2ASK}}(t)=s(t)\cos{\omega_{c}t}
\]
\[
s(t)=\sum_{n}a_{n}g(t-n T_{s})
\]
即控制载波的幅度
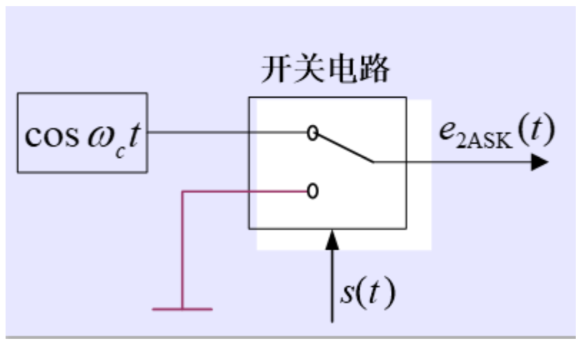
产生方法—一般用电子开关
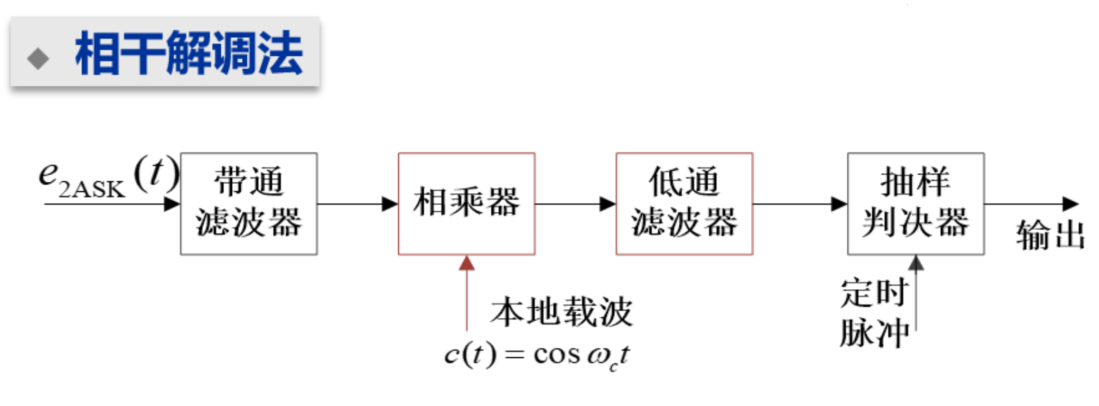
解调方法
通过包络检波
即带通滤噪后全波整流,再经过低通滤波,最后抽样判决
【全波整流 + 低通滤波】=【包络检波器】
后面你会发现,他们长的都差不多捏
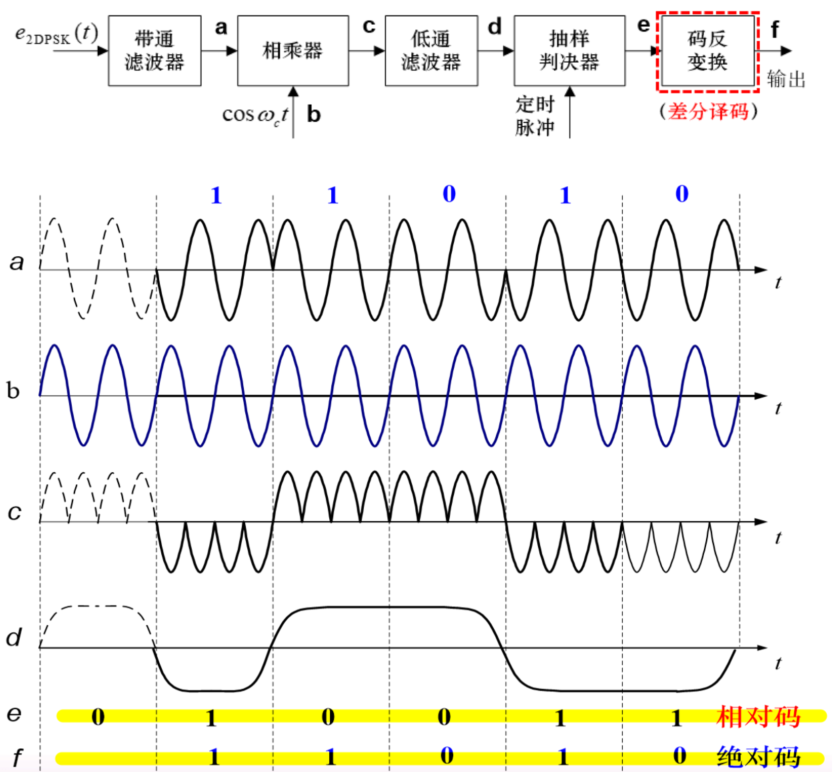
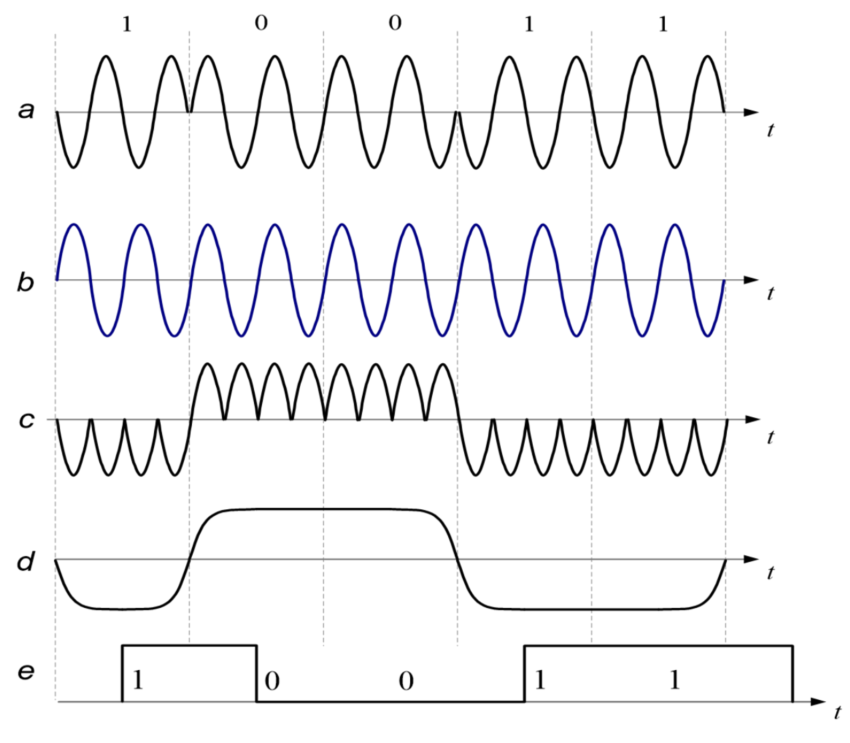
原理框图与每一级波形
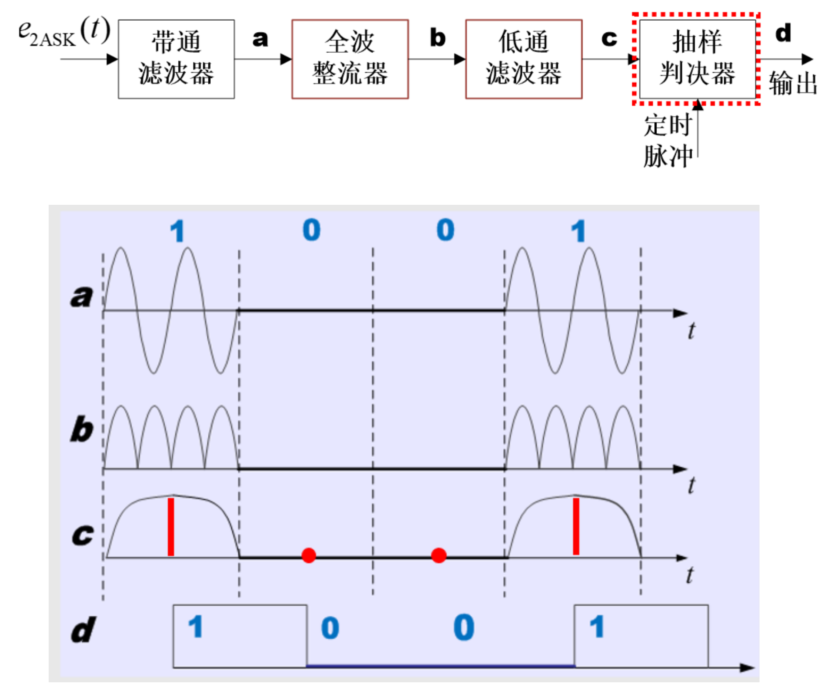
注意,当传输【1101】时,c 路信号的区别,可别是三个通带
俩!土想想第一个和第二个中间怎么可能会凹下去?
d 路输出因采样位置会有一定的时延,考试的时候考不考虑时延?【随意】
本振需要同频同相
相干解调标配:乘法器 + 低通滤去高频分量
不同步的本地载波?
令混频后的信号为 \(m(t)\) ,则经过混频器后有
\[
m(t)=e_{2A S K}(t)\cos\omega_{c}t=s(t)\cos\omega_{c}t\cdot\cos\omega_{c}t
\]
和差化积,过 LPF 后得
\[
m(t)={\frac{1}{2}}s(t)
\]
\[
m(t)=e_{2A S K}(t)\cos\omega_{c}t=s(t)\cos\omega_{c}t\cdot\cos(\omega_{c}t+\Delta\phi)
\]
积化和差,过 LPF 后得
\[
m(t)=\frac{\cos\Delta\phi}{2}s(t)
\]
表现为幅值出现衰减,可能越过门限电平
QPSK 则表现为信号点沿圆周偏离一定相角,即有 bias(复数 e)
\[
m(t)=e_{2A S K}(t)\cos\omega_{c}t=s(t)\cos\omega_{c}t\cdot\cos((\omega_{c}+\Delta\omega)t)
\]
积化和差,过 LPF 后得
\[
m(t)={\frac{\cos\Delta\omega t}{2}}s(t)
\]
表现为接受信号时变,甚至发生翻转
QPSK 则表现为信号点沿圆周以一定速度绕圈圈
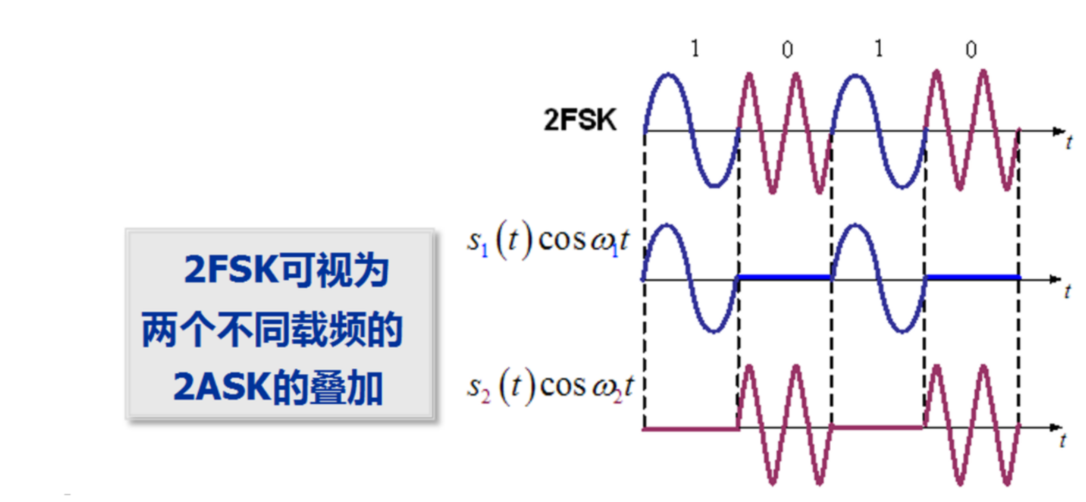
二进制频移键控(2FSK)
在数字通信中应用较为广泛,尤其适用于衰落信道(如短波无线电信道)的场合
国际电信联盟(TTU)建议在数据率低于 1200 b/s 的场合采用 2FSK 体制。
表达式
\[
e_{\mathrm{2FSK}}(t)=s_{1}(t)\cos\omega_{1}t+s_{2}(t)\cos\omega_{2}t
\]
即控制载波在不同码元下的载频
产生方式
可视为俩 2ASK 的【非】关系之和
所以需要一个反相器
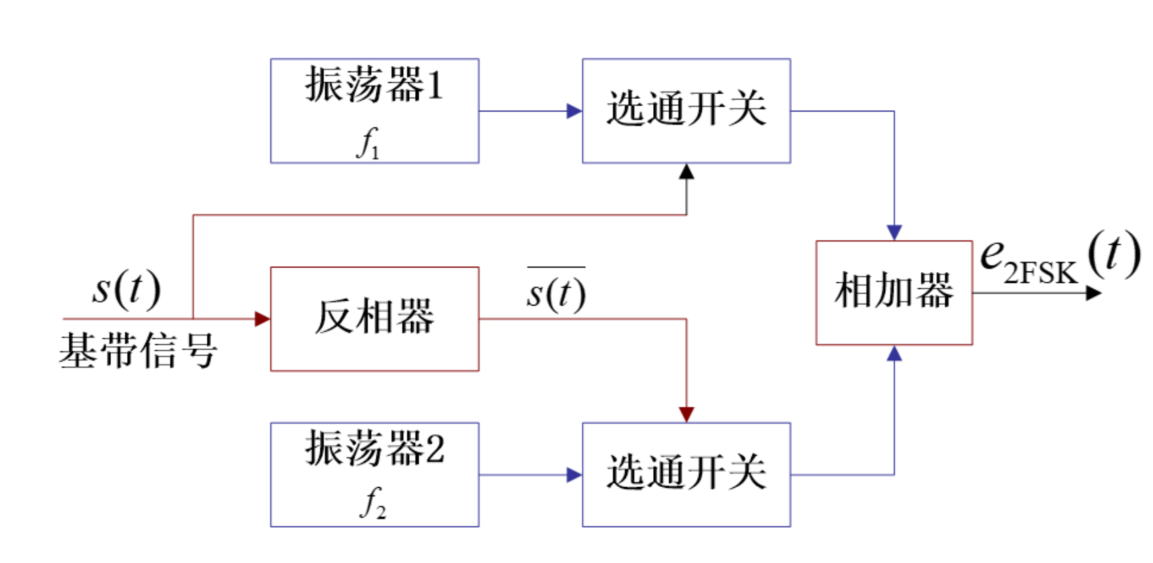
相较于模拟调频,SK 的速度更快、电路简单、波形保真、频率稳定高
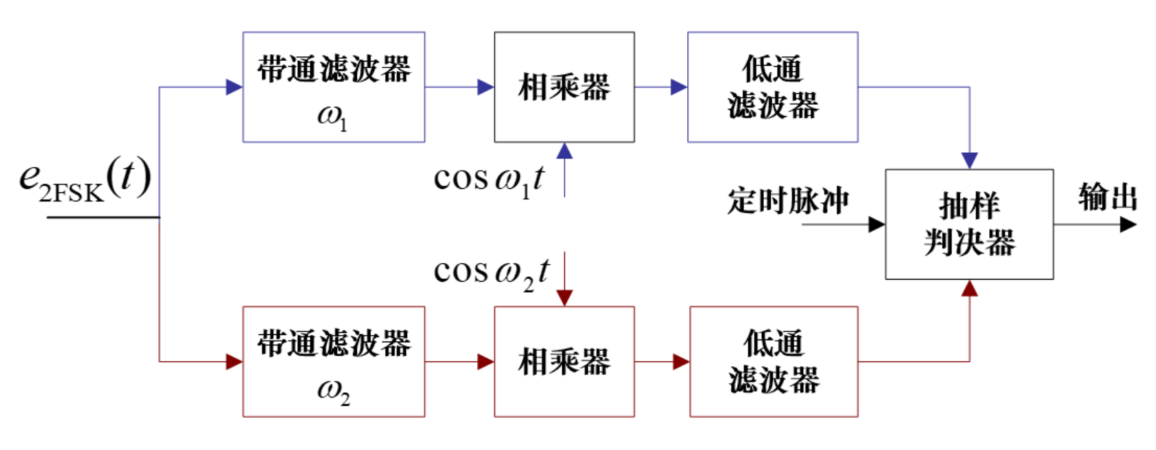
解调方法
- 包络检波
就是俩路 2ASK 解调,关键在 BPF 的通带不同
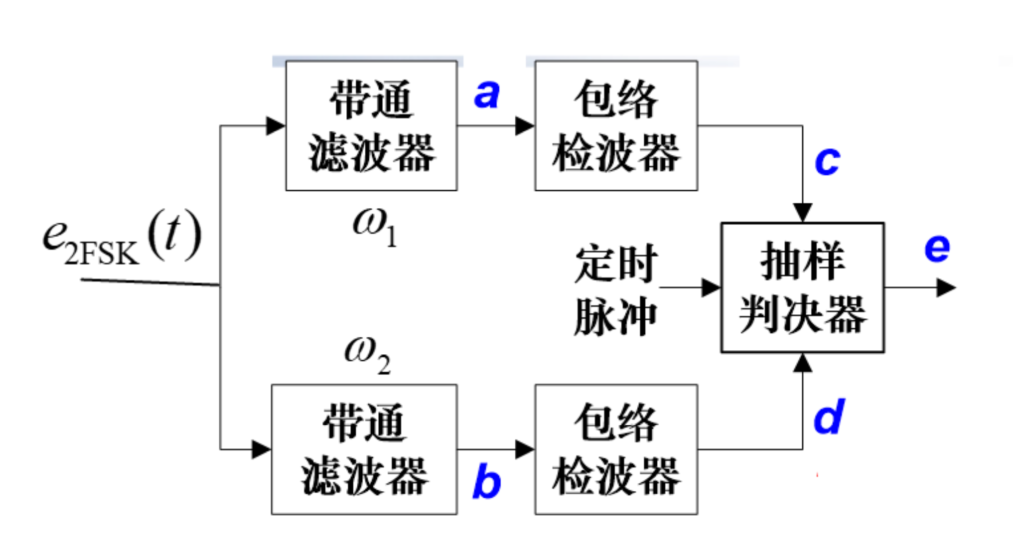
抽样判决有些许不同
两路信号在每一个时刻一定是一 1 一 0,则做减法得 \(+1/-1\)
那么规定所得结果与信息之间的映射即可
- 过零检测法
基本思想:频率与过零点密度正相关,在过零点创建冲激函数再低通
解决两载波频段相近无法带通的问题
故框图顺序为【带通、限幅放大、微分、整流、展宽、低通】
不需要硬记忆,理解了就能大差不差的写出来
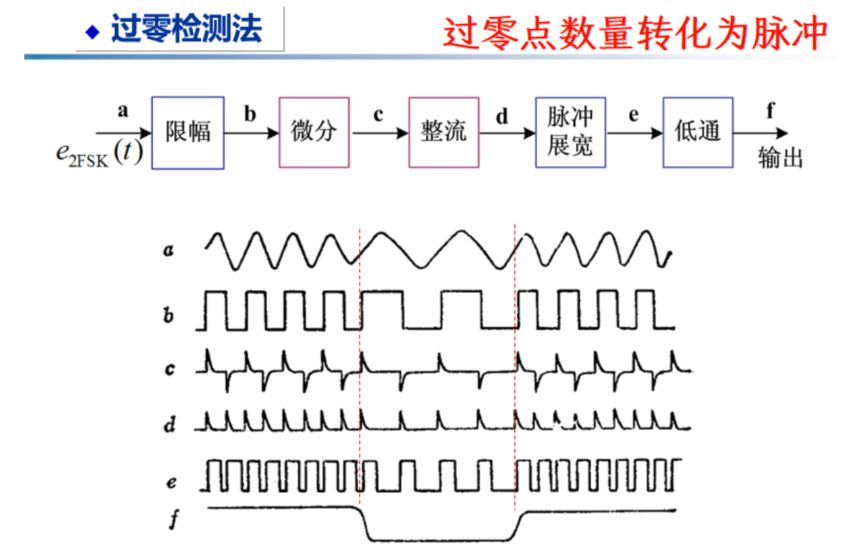
小 SNR 下这一非相干解调方法精度一般般
与包络检波类似,把【包络检波器】置换成【相乘器 +LPF】
关于包络检波
上述方法能使用包络检波
要么是在对幅值调制—2ASK
要么是经过不同的 BPF—2FSK
根本上,是因为存在幅值的差异
而下面的 PSK,因为幅度区别,所以和包络检波 say byebye 啦~
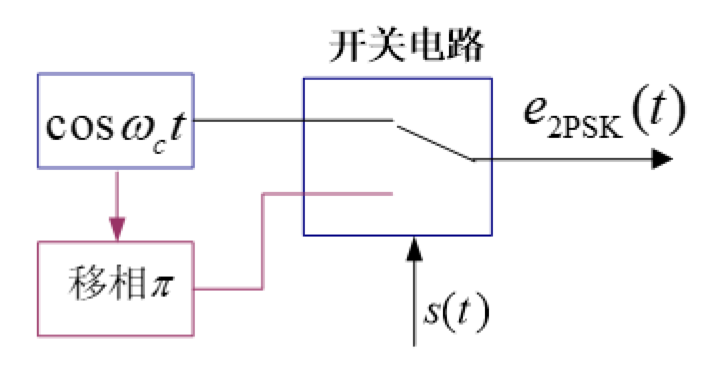
二进制频移键控(2PSK)
表达式
\[
e_{2\mathrm{PSK}}(t)=\mathrm{A}\cos(\omega_ct+\varphi_n)\\\varphi_{n}=\begin{cases}0,&\text{发“}0\text{”时}\\\pi,&\text{发“}1\text{”时}&\end{cases}
\]
即控制载波相位
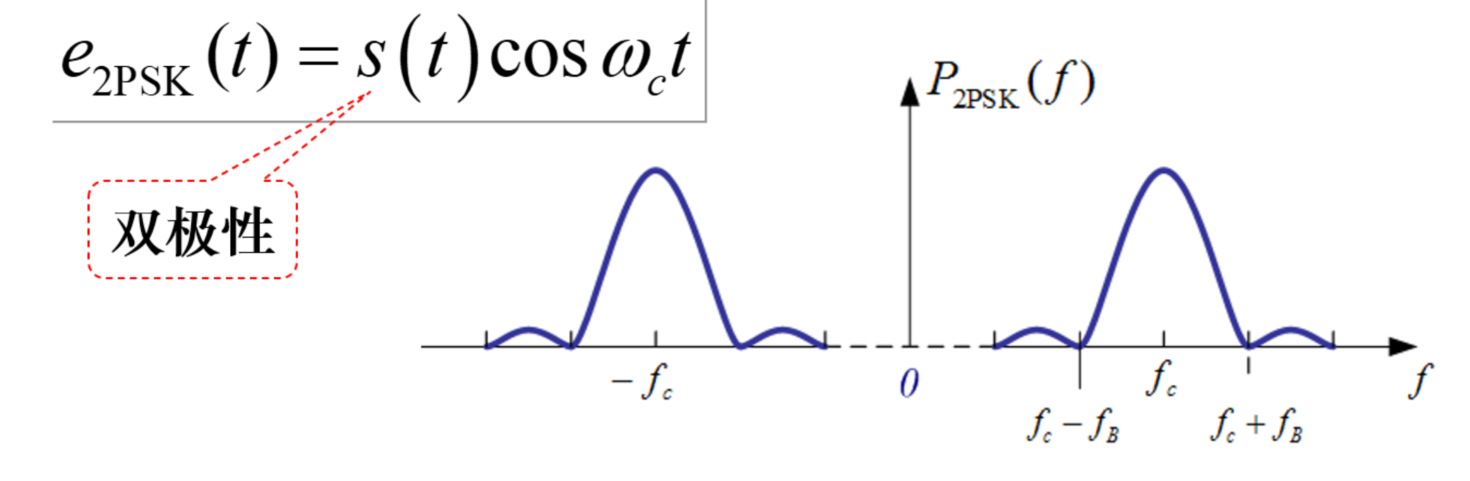
特殊的,这是双极性
产生方式
解调方式
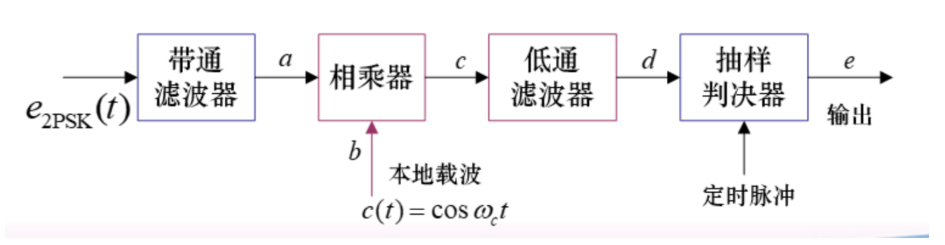
c 路信号直接从时域分析,同号相乘为正,否则为负,01 解码则是自己定啦
2PSK 存在载波锁相时倒 π的问题(这在无差错检测位下无法得知),于是有了 DPSK
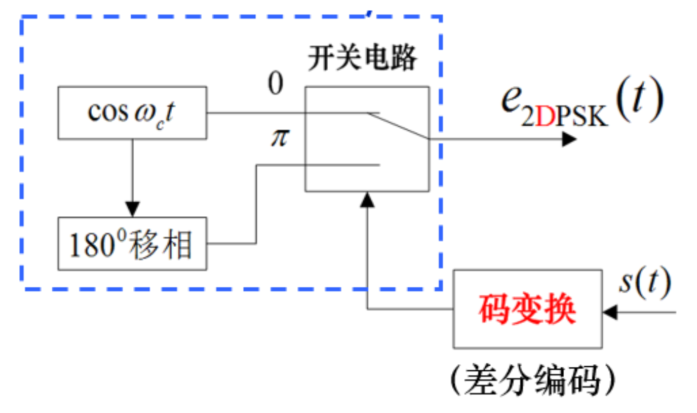
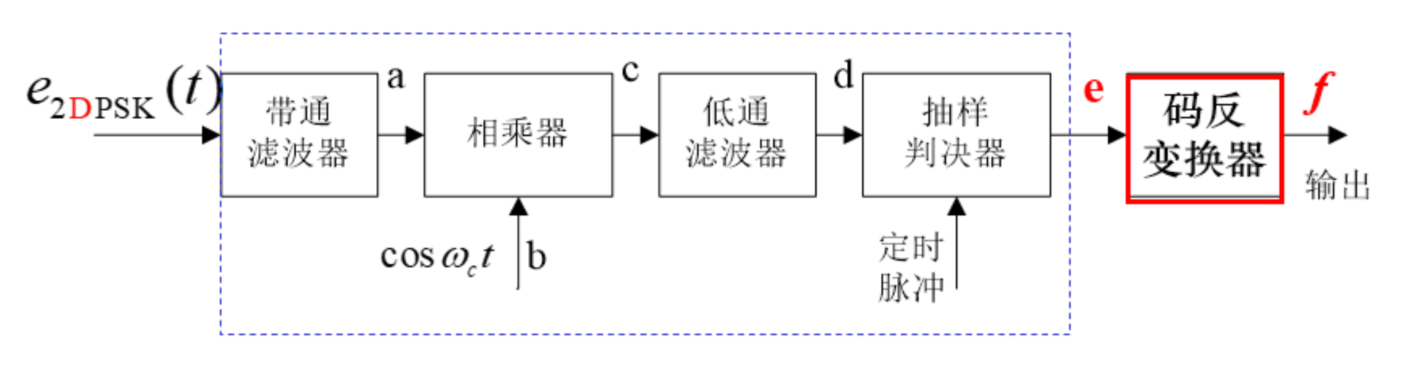
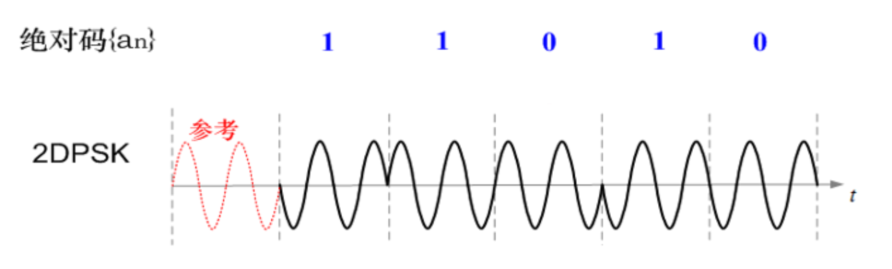
二进制差分相移键控 (2DPSK)
利用相邻的载波相位差表示信息
类似拳头手掌差分码
遇绝对码 1 则相对码反相,即与前一个异或
调制信号全部反向时,对解码没有影响
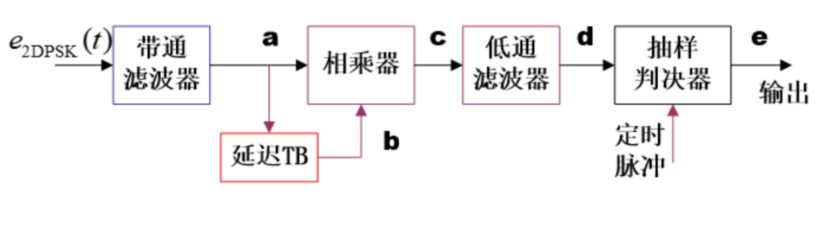
产生方式
多了个码变换
解调方式
比 PSK 多了【码反变换】
利用延时自异
免去载波,故为非相干解调
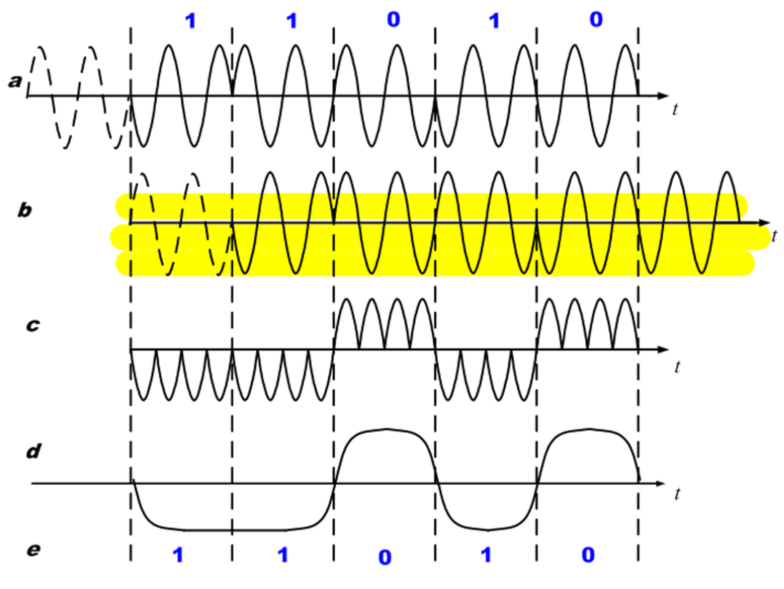
绝对码是 1 则绝对前后相反,过 LPF 后一定是低电平,这是确定的,所以不再需要反码变换啦~
二进制数字调制的 PSD
不得不回想的前置知识
wait a minute🫸 想要优雅的把下面的两节啃完?
那你不得不温习一下(相信你基本上忘记了):
- 上一节课的内容【几种数字调制原理】
- 窄带随机过程【包络相位 | 同向正交 | 统计特性 | 瑞利分布 |Rise 分布 | 高斯分布】
- 基带信号的 PSD【交变波、连续谱 | 稳态波、离散谱 | 零点位置】
- 二进制单/双极性抗造性能分析【概率密度函数 | 误码率计算 | 最佳门限 |(补)误差函数 \(erf(x)\)】
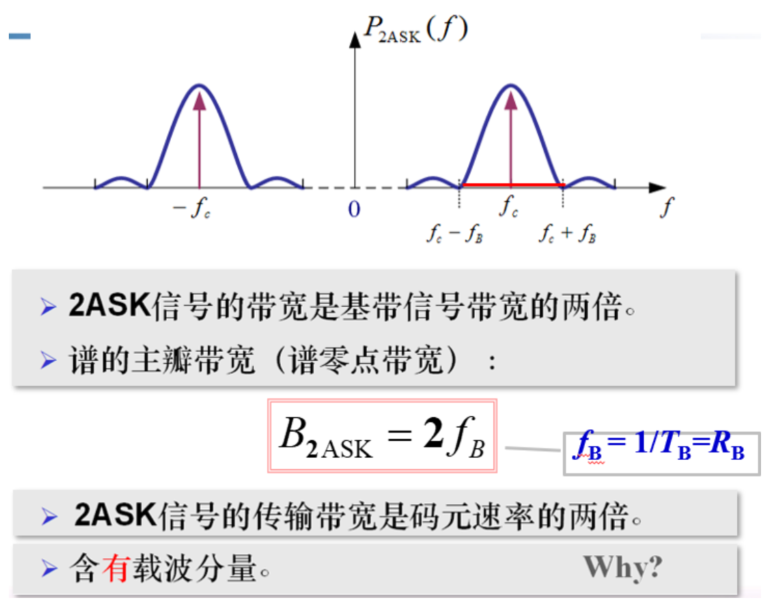
2ASK
时域/功率谱表达式
\[
\boxed{e_{\mathrm{2ASK}}(t)=s(t)\cos\omega_{c}t}
\]
\[
P_{\mathrm{2ASK}}(f)=\frac{1}{4}\Big[P_{s}(f+f_{c})+P_{s}(f-f_{c})\Big]
\]
- 系数为 0.5(s(t)coswt,功率变为原来一半) \(^{\star}0.5\) (频谱搬移,双边谱减半)\(=\frac{1}{4}\)
- 线性调制(没有产生新的频谱分量)
注意,含有载波分量(单极性下有离散谱的载波分量 | 非归零码) | 频带利用率\(\eta=\frac{1}{2}\)
2PSK/2DPSK
频谱与带宽和 2ASK 一致
\[
P_{2\mathrm{PSK}}(f)=\frac{1}{4}\Big[P_{s}(f+f_{c})+P_{s}(f-f_{c})\Big]
\]
\[
B_{\mathrm{2DPSK}}=B_{\mathrm{2PSK}}=2f_{B}
\]
无离散谱分量(双极性),无载波分量【频带利用率】| 频带利用率也是 0.5
2FSK
表达式
\[
e_{2F S K}(t)=s_{1}(t)\cos\omega_{1}t+s_{2}(t)\cos\omega_{2}t
\]
故 PSD 为俩 PSD 合成
\[
\begin{array}{r}{P_{\mathrm{2FSK}}(f)=\cfrac{1}{4}\Big[P_{s_{1}}(f-f_{1})+P_{s_{1}}(f+f_{1})\Big]}\\ {+\cfrac{1}{4}\Big[P_{s_{2}}(f-f_{2})+P_{s_{2}}(f+f_{2})\Big]}\end{array}
\]
带宽为载波差 + 两倍带宽,即
\[
B_{2\mathrm{FSK}}\approx|f_{2}-f_{1}|+2f_{B}
\]
当间距为带宽时,是单峰与双峰的分界线
频带利用率
\[
\frac{R_{B}}{B_{2F S K}}=\frac{f_{B}}{|f_{2}-f_{1}|+2f_{B}}
\]
例
设某 MPSK 系统的比特率为 4800bps,并设基带信号采用 a=1 余弦滚降滤波预处理
(1)4PSK 占用的信道带宽和频带利用率;
(2)8PSK 占用的信道带宽和频带利用率。
- \(B={\frac{(1+\alpha)R_{\mathrm{b}}}{\log_{2}M}}={\frac{(1+1)\times4800}{\log_{2}4}}=4800(\mathrm{Hz})\)
\(\eta_{\mathrm{b}}=\frac{\log_{2}M}{(1+\alpha)}=\frac{\log_{2}4}{1+1}=1\left(\mathrm{b}/(\mathrm{s}\cdot\mathrm{Hz})\right)\)
- \(B={\frac{(1+\alpha)R_{\mathrm{b}}}{\log_{2}M}}={\frac{(1+1)\times4800}{\log_{2}8}}=3200(\mathrm{Hz})\)
\(\eta_{\mathrm{b}}=\frac{\log_{2}M}{(1+\alpha)}=\frac{\log_{2}8}{1+1}=1.5(\mathrm{b}/(s\cdot \mathrm{Hz}))\)
注意
\(R_{B}={\frac{R_{b}}{\log_{2}M}}\)
在 PSK 中 ,调制后带宽 \(B=2(1+\alpha)f_{N}=(1+\alpha)R_{B}={\frac{(1+\alpha)R_{\mathrm{b}}}{\log_{2}M}}\)
频带利用率也有俩种,视题目条件而定
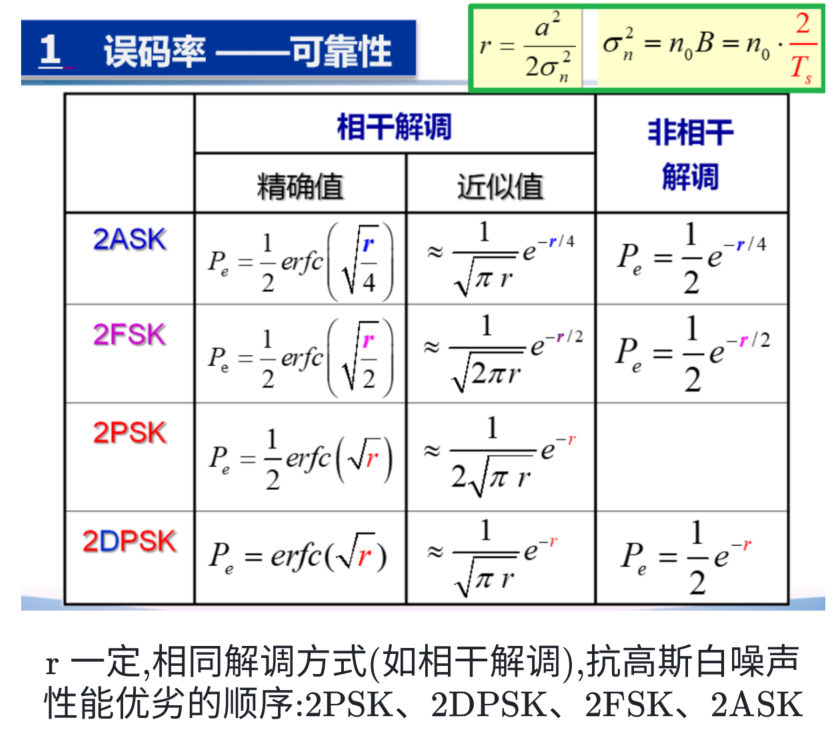
二进制调制系统的抗噪性能
需要知道分析逻辑,具体公式考试会给出
即不需要你背,但需要你知道有这些东东(可以计算结果的参数)
猴急的同学可以直接快进到性能比较
会保留推导过程,有兴趣可以看看,帮助记忆
别说刚刚看过又忘记啥是【恒参信道】 【窄带高斯白噪】了 😆
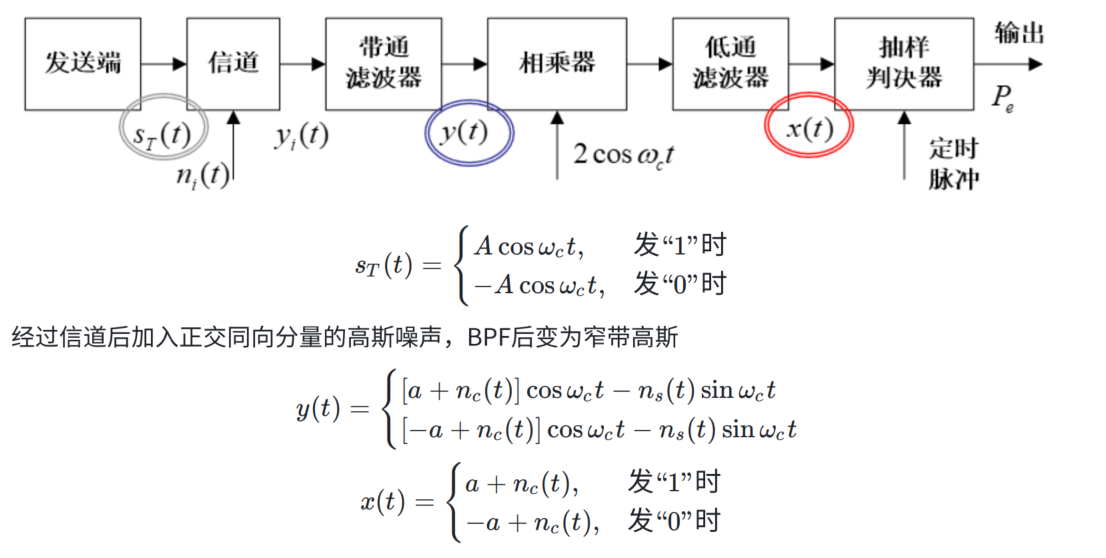
2ASK
令发送信号为
\[
\left.s_T\left(t\right)=\left\{\begin{array}{cc}A\cos\omega_ct,&\text{发“l”时}\\0&\text{发“0”时}\end{array}\right.\right.
\]
则经过信道后
\[
y_i(t)=\begin{cases}a\cos\omega_ct+n_i(t)&\text{发“1”时}\\0+n_i(t)&\text{发“0”时}&\end{cases}
\]
没有信号时只有高斯白噪
此处的 \(a=K A\) ,需要经过信道估计求得
经过 BPF 后留下有用信号与窄带高斯
\[
y(t)=\begin{cases}a\cos\omega_ct+n(t)&\text{发“1”时}\\0+n(t)&\text{发“0”时}&\end{cases}
\]
回顾一下二进制单极性的抽样判决
\[
\left.x(kT_B)=\left\{\begin{array}{ll}A+n_R(kT_B),&\mathrm{“l”}\\0+n_R(kT_B),&\mathrm{“}0\end{array}\right.\right.
\]
不能说相差无几,只能说一模一样
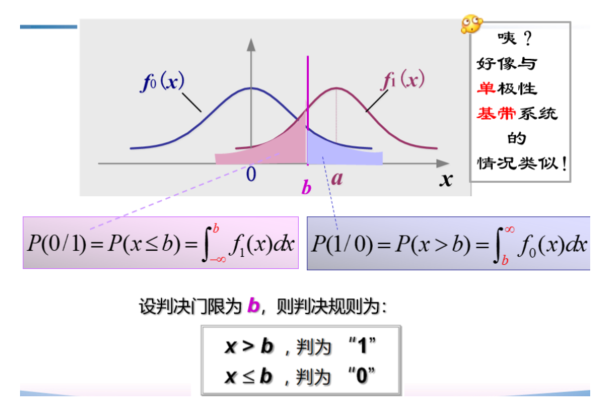
再回顾一下二进制单极性基带系统误码率
\[
P_{e}=\frac{1}{2}e r f c(\frac{A}{2\sqrt{2}\sigma_{n}})
\]
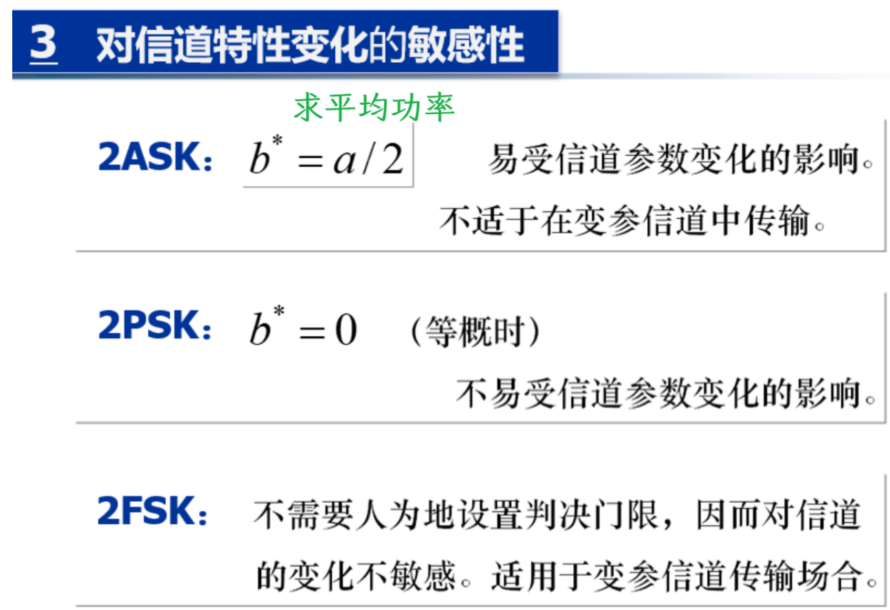
2ASK 也是一样的,只不过把 \(\mathsf{A}\) 改成了经过信道的 a
\[
P_{e}=\frac{1}{2}e r f c(\frac{a}{2\sqrt{2}\sigma_{n}})
\]
最佳判决门限
\[
V_{d}^{*}=\frac{a}{2}+\frac{\sigma_{n}^{2}}{a}\ln\frac{P(0)}{P(1)}
\]
令解调器输入端信噪比为 r,则
\[
r=\frac{a^{2}}{2\sigma_{n}^{2}}
\]
介就是E_b/N_0,数字信噪比
那么代入得
\[
P_{e}={\frac{1}{2}}e r f c\Big(\sqrt{r/4}\Big)
\]
注意这里是 【补误差函数】
当 \(\mathsf{r}\!>\!\!10\) 时,有近似
\[
P_{e}\approx{\frac{1}{\sqrt{\pi r}}}e^{-r/4}
\]
感觉有点像把积分拿掉了,再乘 \(\frac{1}{\sqrt{r}}\)
同样的,经过 BPF 后有
\[
y(t)=\begin{cases}a\cos\omega_ct+n(t)&\text{发“1”时 }\sim\text{正弦波}+\text{窄带高斯噪声}\\0+n(t)&\text{发“}0\text{”时 }\sim\text{窄带高斯噪声}&\end{cases}
\]
但略有不同的是,包络检波为 | 取模 | 操作,在数学上为【和角】
于是把噪声拆成【同向正交形式】,即
\[
n(t)=n_{c}(t)\cos\omega_{c}t-n_{s}(t)\sin\omega_{c}t
\]
根据前置知识,我们知道
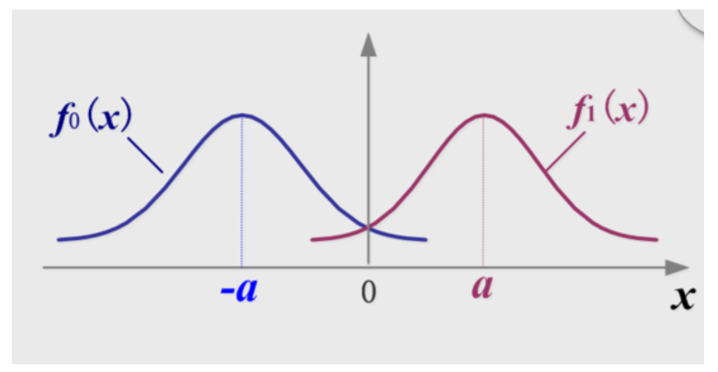
【正弦信号 + 高斯窄带噪声 \(\sim\) 广义瑞利分布】【高斯窄带噪声 \(\sim\) 瑞利分布】【高 SNR 下=高斯分布】
即在发 1 时检波器输出为
\[
V(t)=\sqrt{[a+n_{c}(t)]^{2}+n_{s}^{2}(t)}
\]
则分布服从广义瑞利分布
\[
f_{1}(V)=\frac{V}{\sigma_{n}^{2}}I_{0}\left(\frac{a V}{\sigma_{n}^{2}}\right)e^{-(V^{2}+a^{2})/2\sigma_{n}^{2}}
\]
\(I_{0}(x)\) 是零阶修正贝塞尔函数;当 \(x\geq0\) 时, \({\cal I}_{0}(x)\) 单调上升,且 \(I_{0}(0)=1\)
而发送 0 时
\[
V(t)=\sqrt{n_{c}^{2}(t)+n_{s}^{2}(t)}
\]
服从瑞利分布
\[
f_{0}(V)=\frac{V}{\sigma_{n}^{2}}e^{-V^{2}/2\sigma_{n}^{2}}
\]
下面是判决过程推导,就不打扰了,安静看图
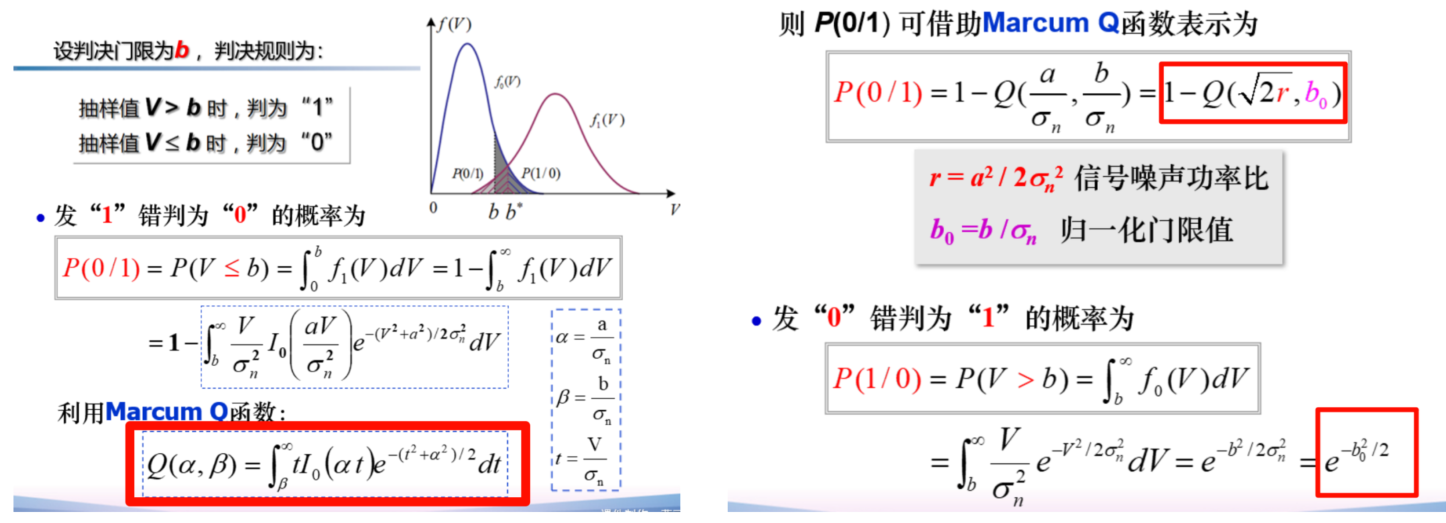
- Marcum Q 函数,用于广义瑞利分布(Rise 分布)| 最后用
r&b 表示
- 瑞利分布可直接求解
得误码率
\[
\begin{array}{l}{P_{e}=P(1)P(0/1)+P(0)P(1/0)}\\ {\qquad=P(1)\Big[1-Q(\sqrt{2r},b_{0})\Big]+P(0)e^{-b_{0}^{2}/2}}\end{array}
\]
等概下为
\[
P_{e}=\frac{1}{2}\Big[{\bf1}-Q(\sqrt{2r},b_{0})\Big]+\frac{1}{2}e^{-b_{0}^{2}/2}
\]
最佳判决门限

实际情况:当 SNR 很很大时,近似服从高斯分布
故最佳判决门限在中间的位置,即【a/2】
此时的误码率为
\[
P_{e}={\frac{1}{4}}e r f c\!\left({\sqrt{\frac{r}{4}}}\right)+{\frac{1}{2}}e^{-r/4}
\]
再工程一些,有
\[
P_{e}=\frac{1}{2}e^{-r/4}
\]
总结
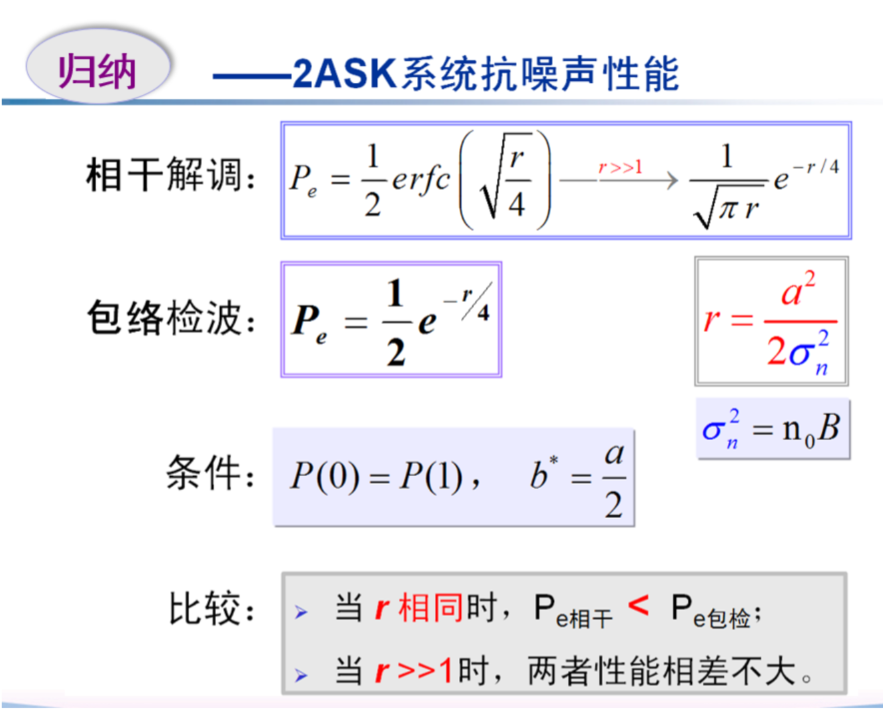
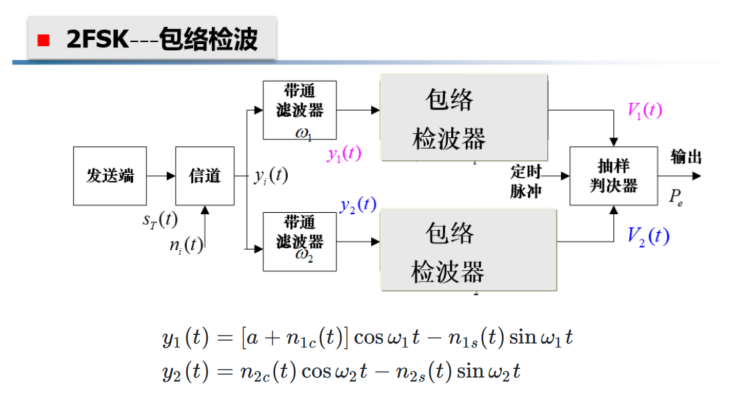
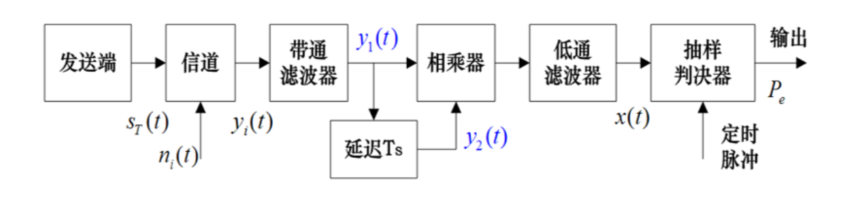
2FSK
也是俩 2ASK 的叠加
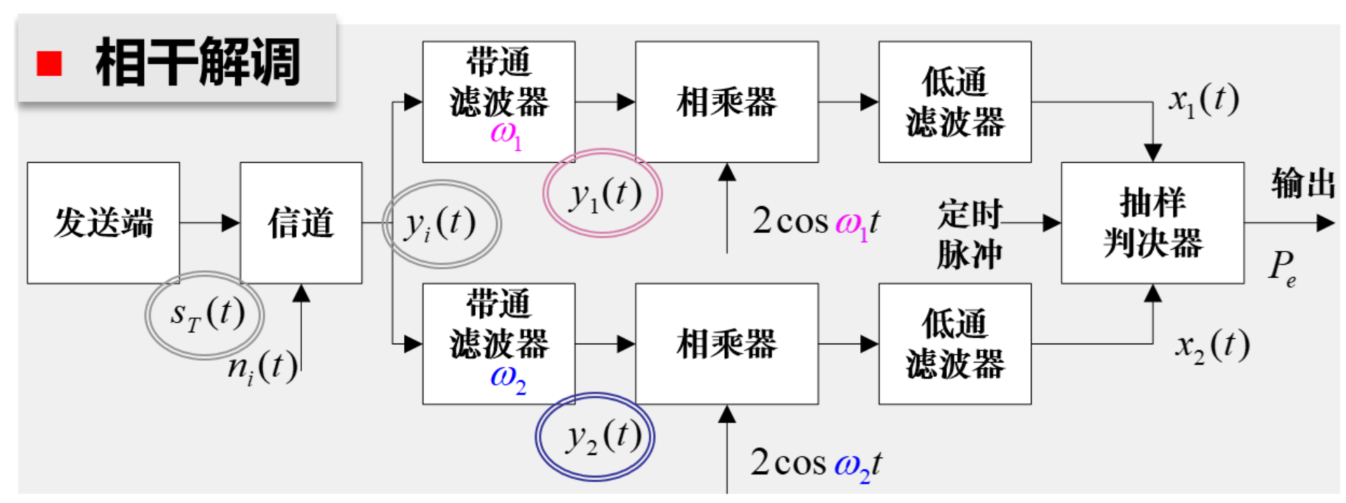
不难推测,经过带通后
\[
\begin{aligned}&y_1(t)=\begin{cases}a\cos\omega_1t+n_1(t)&\text{发“1”时}\\0+n_1(t)&\text{发“0”时}&\end{cases}\\&y_2(t)=\begin{cases}0+n_2(t)&\text{发“0”时}\\a\cos\omega_2t+n_2(t)&\text{发“1”时}&\end{cases}\end{aligned}
\]
转为窄带高斯噪声 白噪声自相关为 0,互相独立
以发送 1 时为例
\[
\frac{y_{1}(t)=a\cos\omega_{1}t+n_{1}(t)}{y_{2}(t)=\quad0\quad+n_{2}(t)}
\]
窄带高斯白噪声
\[
\begin{array}{r}{n_{1}(t)=n_{1c}(t)\cos\omega_{1}t-n_{1s}(t)\sin\omega_{1}t}\\ {n_{2}(t)=n_{2c}(t)\cos\omega_{2}t-n_{2s}(t)\sin\omega_{2}t}\end{array}
\]
我是生怕 自己 你忘记了呀
窄带随机过程告诉我们,噪声与其正交/同向分量的均值,方差都相同,且互相独立
相干解调后,俩都是高斯

错判概率
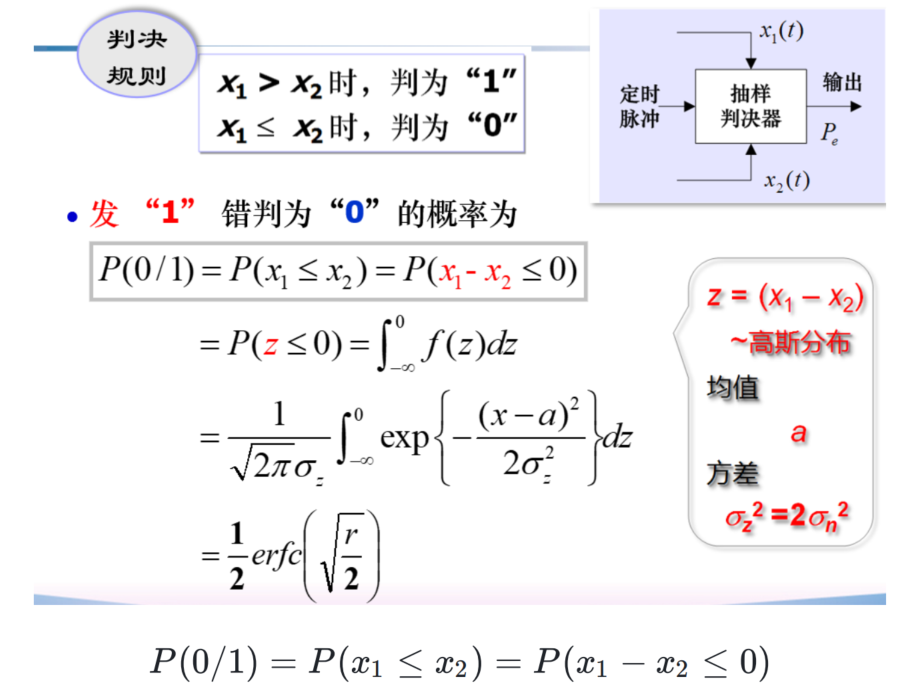
神之一手:俩高斯的线性组合还是高斯分布
最后得
\[
{\frac{1}{2}}e r f c\left({\sqrt{\frac{r}{2}}}\right)
\]
因信道对称性,【发 0 判 1】概率相等
\[
P(\mathbf{1}/\mathbf{0})=P(x_{1}>x_{2})=\frac{\mathbf{1}}{2}e r f c\biggl(\sqrt{\frac{r}{2}}\biggr)
\]
总误码率
\[
P_{\mathrm{{e}}}={\frac{1}{2}}e r f c{\Bigg(}{\sqrt{\frac{r}{2}}}{\Bigg)}
\]
高 SNR 下,有近似
\[
\frac{1}{\sqrt{2\pi r}}e^{-r/2}
\]
牺牲更多功率,换更小的误码率
同样的,有 Rise 分布与瑞利分布
利用独立计算边缘概率密度函数求分布

所以误码率为
\[
P_{e}=\frac{1}{2}e^{-r/2}
\]
例
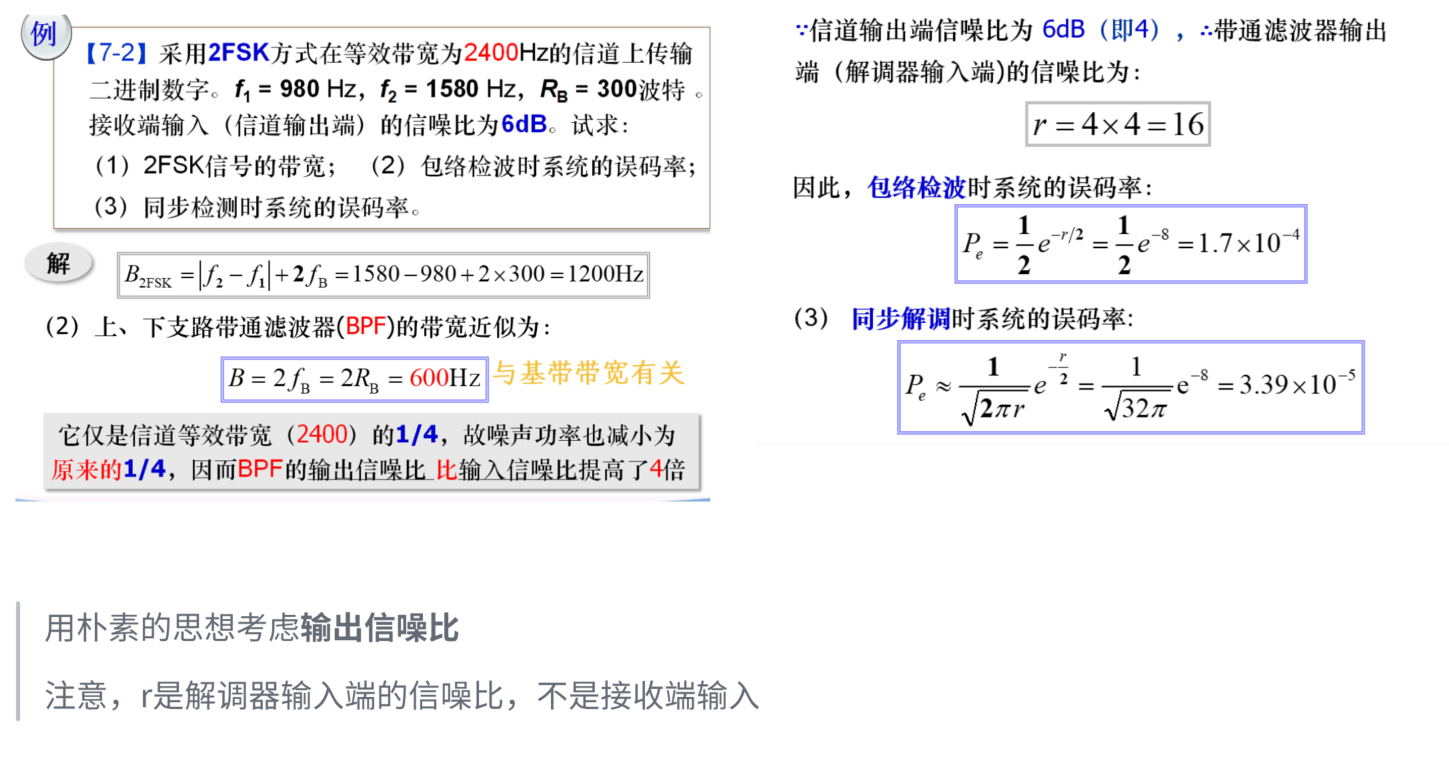
2PSK/2DPSK
2PSK
与二进制双极性基带系统误码率推导相似
为俩轴对称高斯分布
最佳判决门限
\[
V_{d}^{*}=\frac{\sigma_{n}^{2}}{2a}\ln\frac{P(0)}{P(1)}
\]
误码率
\[
P_{e}={\frac{1}{2}}e r f c({\frac{a}{\sqrt{2}\sigma_{n}}})={\frac{1}{2}}e r f c(\sqrt{r})
\]
大 SNR 下有近似
\[
P_{e}\approx{\frac{1}{2{\sqrt{\pi r}}}}e^{-r}
\]
2DPSK 码反变换
e 端口为 2PSK 误码率
\[
\boxed{P_{e2\mathrm{PSK}}=\cfrac{1}{2}e r f c\left(\sqrt{r}\right)\approx\cfrac{1}{2\sqrt{\pi r}}e^{-r}}
\]
则
\[
P_{e}^{'}=(1-P_{e})P_{e}+P_{e}(1-P_{e})=2P_{e}(1-P_{e})
\]
在大 SNR 下,误码率远小于 1,故
\[
P_{e2D P S K}^{'}\approx2P_{e}\approx\frac{1}{\sqrt{\pi r}}e^{-r}
\]
2DPSK 相位比较
这里有点抽象
设 当前发送 1 ,且令前一个码元也是 1(或 0)则 送入相乘器的两个信号 \(y_{1}(t)\) 和 \(y_{2}(t)\) 可表示为 :
\[
\begin{array}{r}{y_{1}(t)=a\cos\omega_{c}t+n_{1}(t)=[a+n_{1c}(t)]\cos\omega_{c}t-n_{1s}(t)\sin\omega_{c}t}\\ {y_{2}(t)=a\cos\omega_{c}t+n_{2}(t)=[a+n_{2c}(t)]\cos\omega_{c}t-n_{2s}(t)\sin\omega_{c}t}\end{array}
\]
\[
n_1(t)\text{为叠加在前一码元上的窄带高斯噪声}\\n_2(t)\text{为叠加在后一码元上的窄带高斯噪声}
\]
经过 LPF 和抽样后,滤去正交项与高次谐波,有
\[
x={\frac{1}{2}}[(a+n_{1c})(a+n_{2c})+n_{1s}n_{2s}]
\]
发 1 判 0 的概率
\[
P(0/1)=P\{x<0\}=P\{\frac{1}{2}[(a+n_{1c})(a+n_{2c})+n_{1s}n_{2s}]<0\}
\]
利用恒等式
\[
\begin{array}{c}{{x_{1}x_{2}+y_{1}y_{2}=\displaystyle\frac{1}{4}\{\left[\left(x_{1}+x_{2}\right)^{2}+\left(y_{1}+y_{2}\right)^{2}\right]}}\\ {{-\left[\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}\right]\}}}\end{array}
\]
则可以转换为
\[
P\left(0/1\right)=P\{[(2a+n_{1c}+n_{2c})^2+(n_{1s}+n_{2s})^2-(n_{1c}-n_{2c})^2-(n_{1s}-n_{2s})^2]<0\}
\]
观察到前俩项的平方根为【广义瑞利分布】,后者平方根为【瑞利分布】,则只要证明【前后独立】即可拆分计算
即证明俩噪声均方值相同,不是很懂不再赘述
简化为
\[
P(0/1)=P(R_1^2-R_2^2<0)=P(R_1<R_2)
\]
与 2FSK-包络检波 过程相似
最后得
\[
\begin{gathered}P(0/1)=P\{R_1<R_2\}=\int_0^\infty f(R_1)\left[\int_{R_2=R_1}^\infty f(R_2)dR_2\right]dR_1\\=\int_0^\infty\frac{R_1}{2\sigma_n^2}I_0\left(\frac{aR_1}{\sigma_n^2}\right)e^{-(2R_1^2+4a^2)/4\sigma_n^2}dR_1=\frac{1}{2}e^{-r}\end{gathered}
\]
因为
\[
P(1/0)=P(0/1)=\frac{1}{2}e^{-r}
\]
所以其误码率为
\[
\boxed{P_e=\frac{1}{2}e^{-r}}
\]
例

性能比较
nbu 期末最多考这里的结论