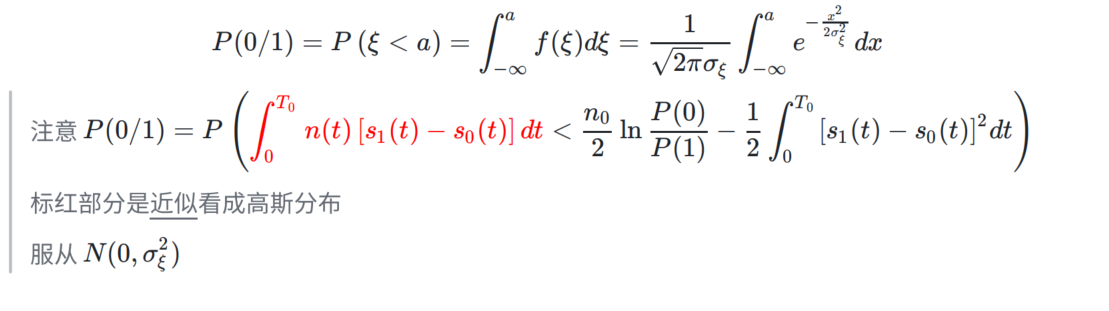数字信号的最佳接收
不同前提条件下的最佳接收定义不同
【最佳】 可能是:
统计特性
以二进制为例 (回忆二进制基带抗噪性能分析)
噪声 n(t)的统计特性
设 \(n(t)\) 是零均值的高斯白噪声
则通过随机信号分析的知识,得到其K维概率密度函数为边缘概率密度函数的乘积,即
\[
\boxed{f(n)=\frac{1}{(\sqrt{2\pi}\sigma_{n})^{k}}\exp\left\{-\frac{1}{2\sigma_{n}^{2}}\sum_{i=1}^{k}n_{i}^{2}\right\}}
\]
这里的概率密度函数是离散的,而我们希望得到连续的过程 \(n(t)\)
设带限信道的截止频率为 \(f_{\mathrm{H}}\) , 则抽样速率为 \(2f_{\mathrm{H}}\)
则在一个码元持续时间 \(T_{B}\) 内共得到 \(k=2f_{H}T_{B}\) 个抽样值
当 K 很大很大时,噪声在一个 \(T_{B}\) 内的平均功率可表示为
\[
{\frac{1}{k}}\sum_{i=1}^{k}n_{i}^{2}={\frac{1}{T_{\mathrm{B}}2f_{H}}}\sum_{i=1}^{k}n_{i}^{2}
\]
高数中已知函数积分的离散近似(这里的平方表示是功率)
\[
\int_{0}^{T_{B}}n^{2}(t)d t\approx\sum n_{i}^{2}\Delta t
\]
在此处环境中 \(\Delta t=\frac{1}{2f_{H}}\) ,则可以得到
\[
\frac{1}{k}\sum_{i=1}^{k}{n_{i}^{2}}=\frac{1}{T_{\mathrm{B}}2f_{H}}\sum_{i=1}^{k}{n_{i}^{2}}=\frac{1}{T_{\mathrm{B}}}\int_{0}^{T_{\mathrm{B}}}{n^{2}(t)d t}
\]
再令单边功率谱密度为 \(n_{0}\) ,代替 \(T_{B}\)
又因为零均值下均方值(功率)与方差相等,即有 \(\sigma_{n}^{2}=n_{0}f_{H}\) ,则可将上式整理为
\[
\frac{1}{2\sigma_{n}^{2}}\sum_{i=1}^{k}n_{i}^{2}=\frac{1}{n_{0}}\int_{0}^{T_{\mathrm{B}}}n^{2}(t)d t
\]
thus,能将 K 维概率密度函数改写为 \((\mathsf{k}\!\to\!\infty)\)
\[
\boxed{f(n)=\cfrac{1}{\left(\sqrt{2\pi}\sigma_{n}\right)^{k}}\exp\left\{-\cfrac{1}{n_{0}}\int_{0}^{T_{\mathrm{B}}}n^{2}(t)d t\right\}}
\]
式中, \(n=(n_{1},n_{2},...,n_{k})\) 为 \(k\) 维矢量,表示一个码元内噪声的 \(k\) 个抽样值,可看作是 \(k\) 维空间中的一个点
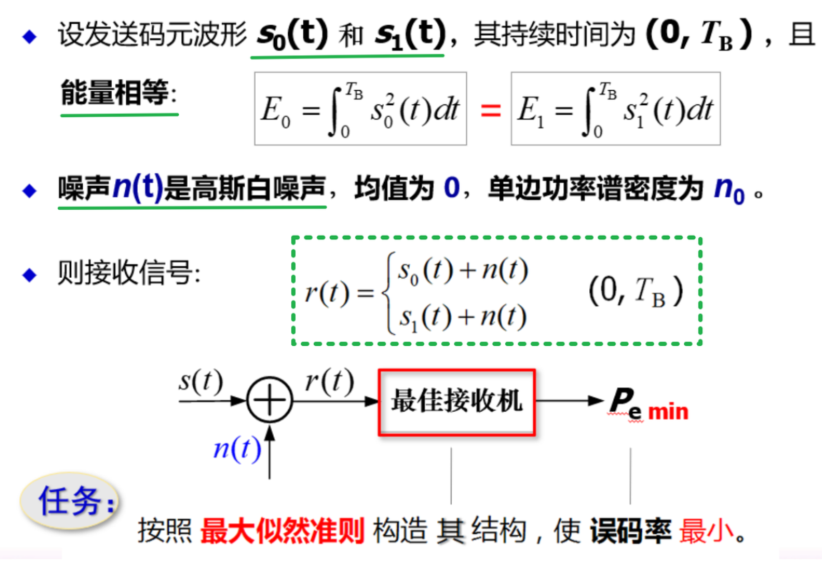
接收信号 r(t) 的统计特性
\[
{r(t)=s(t)+n(t)}
\]
显然,\(r(t)\)也服从高斯分布,均值为 \(s(t)\),方差仍为 \(\sigma_{n}^{2}\)
基于我们惊人的注意力,不难注意到
当出现信号 \(s_{0}(t)\) 时,接收电压 \(r(t)\) 的 \(k\) 维联合概率密度函数
\[
\boxed{f_{0}(r)=\frac{1}{\left(\sqrt{2\pi}\sigma_{n}\right)^{k}}\exp\left\{-\frac{1}{n_{0}}\int_{0}^{T_{\mathrm{B}}}\left[r(t)-s_{0}(t)\right]^{2}d t\right\}}
\]
同理,当出现 \(s_{1}(t)\) 时
\[
\boxed{f_{1}(r)=\frac{1}{\left(\sqrt{2\pi}\sigma_{n}\right)^{k}}\exp\left\{-\frac{1}{n_{0}}\int_{0}^{T_{\mathrm{B}}}\left[r(t)-s_{1}(t)\right]^{2}d t\right\}}
\]
M 进制下
\[
\boxed{f_{i}(r)=\frac{1}{\left(\sqrt{2\pi}\sigma_{n}\right)^{k}}\exp\left\{-\frac{1}{n_{0}}\int_{0}^{T_{\mathrm{B}}}\left[r(t)-s_{i}(t)\right]^{2}d t\right\}\left|(i=1,2,\cdots,\mathrm{M})\right.}
\]
误码率最小下的最佳接收
总误码率求解
与基带计算的区别在于,此处的门限不再是一个常数,而为一个函数(矢量)
冷知识
\(a\prec b\) ,在此处意为【a 先于 b】,同理有 \(a\succ b\)
总误码率为
\[
P_{\mathrm{e}}=P(1)P(0/1)+P(0)P(1/0)
\]
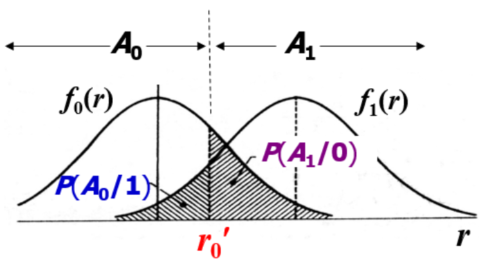
规定分界线 \(r_{0}^{\prime}\)
若接收矢量 \(r\prec r_{0}^{\prime}\) (落在 \(A_{0}\) 域),则判为发送码元是 0
若接收矢量 \(r\succ r_{0}^{\prime}\) (落在 \(A_{1}\) 域),则判为发送码元是 1
则总误码率为
\[
P_{e}=P(1)P(A_{0}/1)+P(0)P(A_{1}/0)
\]
其中
\[
\begin{array}{l}{{P}(A_{0}/1)=P(0/1)=P(\mathbf{r}\leq\mathbf{r}_{0}^{\prime})=\displaystyle\int_{-\infty}^{r_{0}^{\prime}}f_{1}(\mathbf{r})d\mathbf{r}}\\ {P(A_{1}/0)=P(1/0)=P(\mathbf{r}>\mathbf{r}_{0}^{\prime})=\displaystyle\int_{r_{0}^{\prime}}^{\infty}f_{0}(\mathbf{r})d\mathbf{r}}\end{array}
\]
求最佳分界点,即求偏导等于
\[
\boxed{\frac{\partial P_e}{\partial r_0^{^{\prime}}}=0}
\]
整理得
\[
\boxed{\frac{f_0(r_0)}{f_1(r_0)}=\frac{P(1)}{P(0)}}
\]
判决规则为
\[
\boxed{\text{若}\frac{f_0(r)}{f_1(r)}>\frac{P(1)}{P(0)},\quad\text{则判为“}0”\text{若}\frac{f_0(r)}{f_1(r)}<\frac{P(1)}{P(0)},\quad\text{则判为“}1”}
\]
用似然函数判决 0/1(等概下)
\[
\text{若}f_0(r)>f_1(r),\quad\text{则判为“}0"\text{若}f_0(r)<f_1(r),\quad\text{则判为“}1"
\]
即【最大似然准则】
上式交叉相乘得到
\[
P(0)f_{0}(r)=P(1)f_{1}(r)
\]
构造贝叶斯公式计算后验概率
\[
{\frac{P(0)f_{0}(\mathbf{r})}{P(\mathbf{r})}}={\frac{P(\mathbf{1})f_{1}(\mathbf{r})}{P(\mathbf{r})}}
\]
可利用贝叶斯公式 \(f(\theta|x)={\frac{L(x|\theta)f(\theta)}{f(x)}}\) 得到
后验正比于【似然*先验】
无先验,默认为常数(均匀分布)
\[
f_{\mathbf{r}}(\mathbf{0})>f_{\mathbf{r}}(\mathbf{1}),\quad\text{则判为“0”}\\ f_{\mathbf{r}}(\mathbf{0})<f_{\mathbf{r}}(\mathbf{1}),\quad\text{则判为“1”}
\]
即【最大后验概率准则】
\[
\begin{aligned}\text{式中,}&f_\mathrm{r}(1)\text{是收到r后发送“1”的条件概率}\\&f_\mathrm{r}(0)\text{是收到r后发送“0”的条件概率}\end{aligned}\text{称为后验概率}
\]
在高斯白噪下有等价条件
确知数字信号的最佳接收(机)
即相关接收机(以二进制为例)
推导过程,看不懂思密达
已知
\[
\begin{array}{l}{f_{1}(\boldsymbol{r})=\displaystyle\frac{1}{(\sqrt{2\pi}\sigma_{n})^{k}}\exp\left\{-\frac{1}{n_{0}}\int_{0}^{T_{0}}\left[\boldsymbol{r}(t)-\boldsymbol{s}_{1}(t)\right]^{2}d t\right\}}\\ {f_{0}(\boldsymbol{r})=\displaystyle\frac{1}{(\sqrt{2\pi}\sigma_{n})^{k}}\exp\left\{-\frac{1}{n_{0}}\int_{0}^{\pi_{3}}\left[\boldsymbol{r}(t)-\boldsymbol{s}_{0}(t)\right]^{2}d t\right\}}\end{array}
\]
根据
\[
P(0)f_0(r)>P(1)f_1(r),\text{判为 }s_0(t)\\P(0)f_0(r)<P(1)f_1(r),\text{判为 }s_1(t)
\]
代入,两边取对数,再整理得
\[
\int_0^{T_0}r(t)s_0(t)dt+W_0>\int_0^{T_0}r(t)s_1(t)dt+W_1,\text{判为 }s_0(t)\\\int_0^{T_0}r(t)s_0(t)dt+W_0<\int_0^{T_0}r(t)s_1(t)dt+W_1,\text{判为 }s_1(t)
\]
结论
最佳接收结构为r(t)与码元波形混频后积分再比较判决
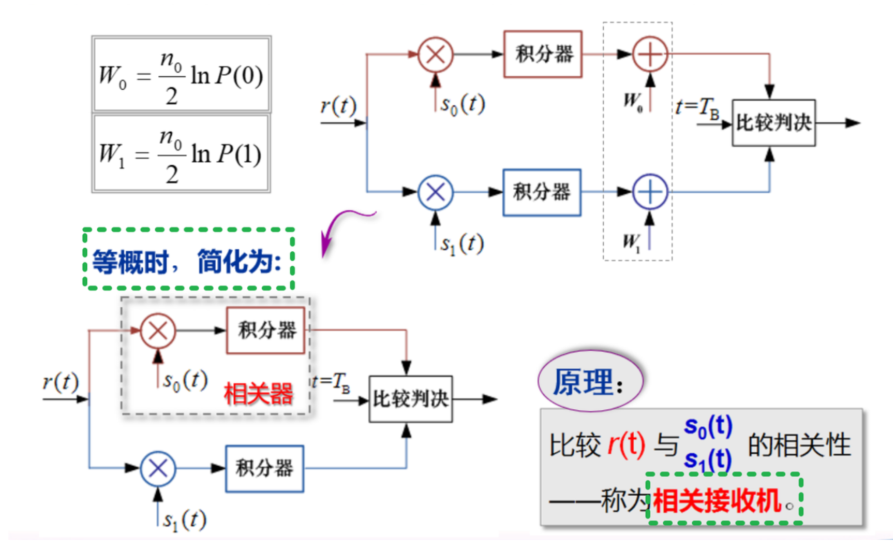
关于相关接收机,需要注意积分器 buffer 每次运算后需要清零,且对符号定时同步讲究
确知数字信号最佳接收机 の 误码率
总误码率
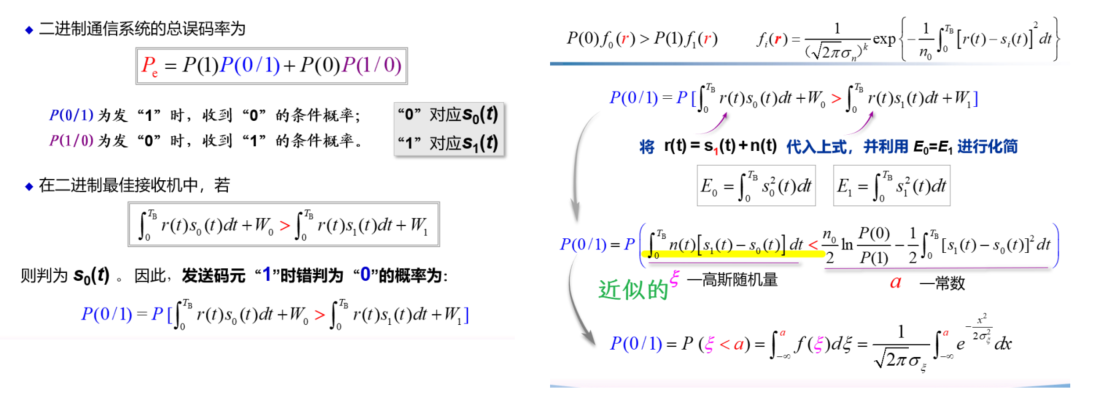
有错判结果
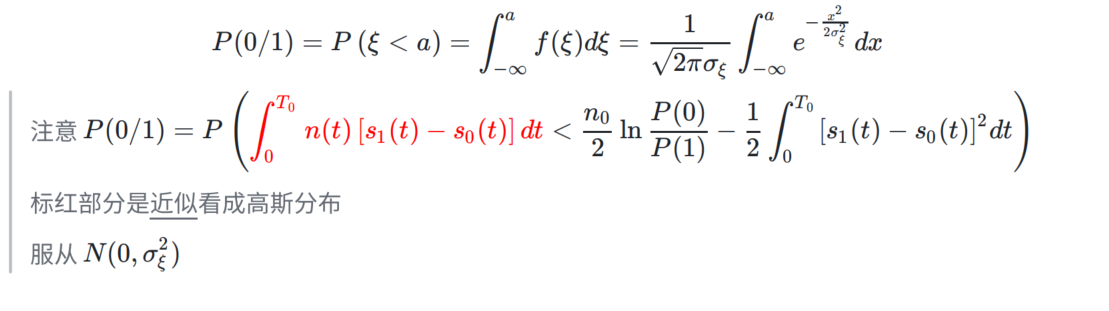
同理有 发0判1
\[
P(1/0)=P(\xi<b)=\int_{-\infty}^bf(\xi)d\xi=\frac{1}{\sqrt{2\pi}\sigma_\xi}\int_{-\infty}^be^{-\frac{x^2}{2\sigma_\xi^2}}dx
\]
式中,b 为
\[
b=\frac{n_{0}}{2}\ln\frac{P(\mathbf{1})}{P(\mathbf{0})}-\frac{\mathbf{1}}{2}\int_{0}^{T_{3}}[s_{0}(t)-s_{1}(t)]^{2}d t
\]
故总误码率为
\[
\boxed{P_{e}=P(1)\frac{1}{\sqrt{2\pi}\sigma_{\xi}}\int_{-\infty}^{a}e^{-\frac{x^{2}}{2\sigma_{\xi}^{2}}}d x+P(0)\frac{1}{\sqrt{2\pi}\sigma_{\xi}}\int_{-\infty}^{b}e^{-\frac{x^{2}}{2\sigma_{\xi}^{2}}}d x}
\]
先验概率对总误码率的影响


误码率仅和两种码元波形之差的能量有关,而与波形本身无关。差别越大,C 值越小,误码率 P 也越小。
\[
c=-\frac{1}{2}\int_{0}^{T_{\mathrm{B}}}[s_{0}(t)-s_{1}(t)]^{2}d t
\]
只与波形之差能量有关,故引入互相关系数
则 \(\mathtt{c}\) 可改写为
\[
\begin{array}{l}{\displaystyle\mathbf{c}=-\frac{1}{2}\int_{0}^{T_{3}}\left[s_{0}(t)-s_{1}(t)\right]^{2}d t}\\ {\displaystyle=-E_{b}(1-\rho)}\end{array}
\]
则误码率可改写为
\[
P_{e}=\frac{1}{2}e r f c\left(\sqrt{\frac{E_{b}(1-\rho)}{2n_{0}}}\right)
\]
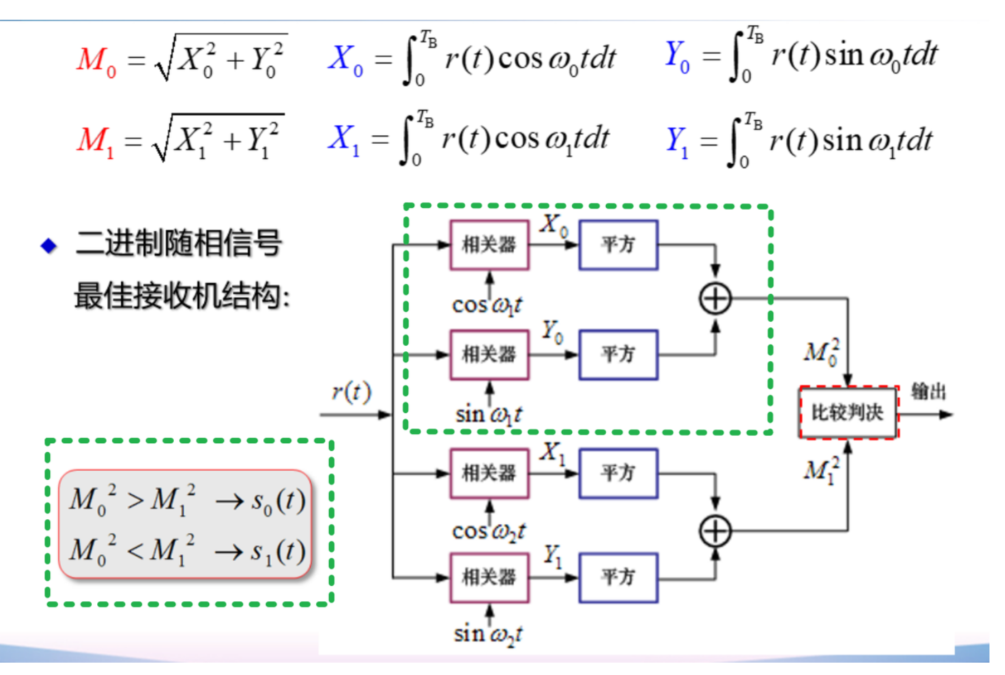
随相数字信号 de 最佳接收
随相,即随机相位(初始相位随机,而码元内信号连续)
最佳接收机结构
通过包络幅值大小判决
得到随相信号的【最佳接收判决规则】
\[
M_0^2>M_1^2,\quad\text{则判为 }s_0(t)\\M_0^2<M_1^2,\quad\text{则判为 }s_1(t)
\]
随相最佳接收机的误码率计算
即有结论
\[
P(1/0)=\frac{1}{2}e^{-\frac{E_{b}}{2n_{0}}}
\]
起伏数字信号最佳接收结构
幅度与相位均为随机变量
基于惊人的注意力,不难发现似然函数为
\[
\begin{array}{l}{{\displaystyle f_{0}({\pmb r})=K^{\prime}\frac{n_{0}}{n_{0}+T_{\mathrm{B}}\sigma_{s}^{2}}\exp\left[\frac{2\sigma_{s}^{2}M_{0}^{2}}{n_{0}\left(n_{0}+T_{\mathrm{B}}\sigma_{s}^{2}\right)}\right]}}\\ {{\displaystyle f_{1}({\pmb r})=K^{\prime}\frac{n_{0}}{n_{0}+T_{\mathrm{B}}\sigma_{s}^{2}}\exp\left[\frac{2\sigma_{s}^{2}M_{1}^{2}}{n_{0}\left(n_{0}+T_{\mathrm{B}}\sigma_{s}^{2}\right)}\right]}}\end{array}
\]
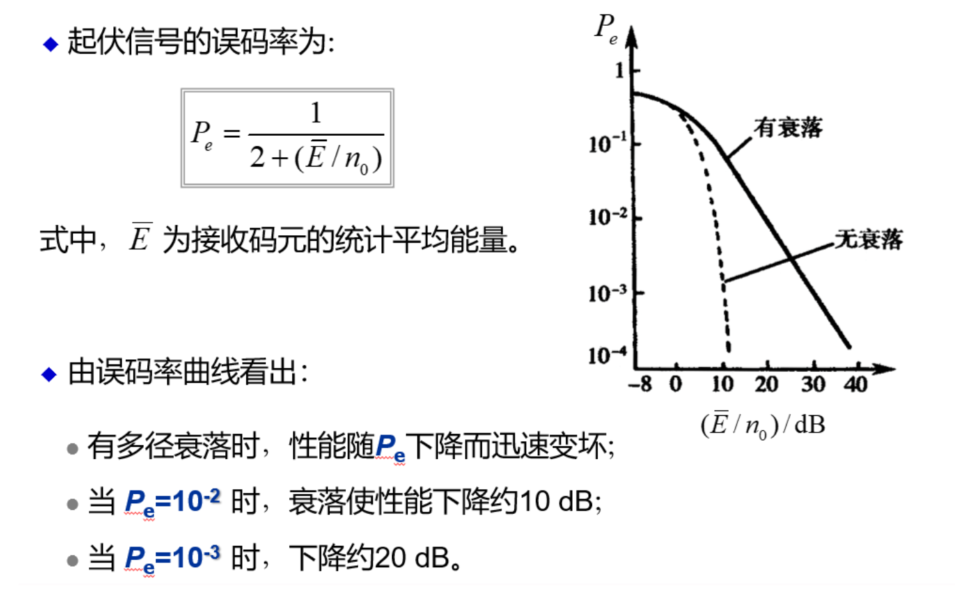
起伏信号的误码率
实际与最佳接收机的性能比较
理论一致,理想下 \(r=\frac{E_{b}}{n_{0}}\)
匹配滤波接收
这一章的计算题考点 (也可能是唯一考点)
匹配滤波器:使得在抽样时刻上获得最大 SNR的线性滤波器,常在发送和接收端放置参数匹配的 RRC,做 pulse shape
本节讨论均在高斯白噪声的前提下
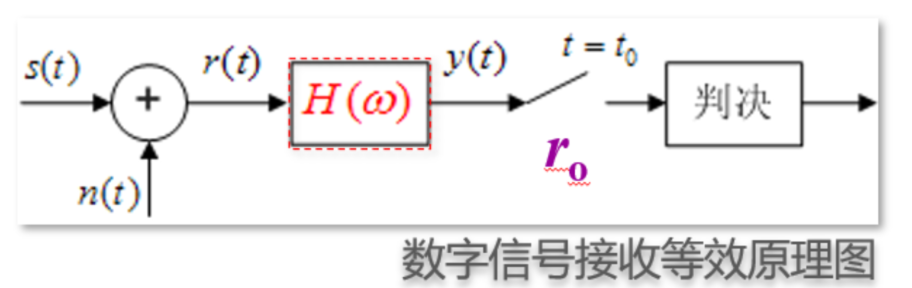
设计 \(H(\omega)\)使其输出信噪比\(r_{0}\) 在抽样时刻\(t_{0}\)有最大值
至于\(t_{0}\) 到底是啥时候取决于符号定时同步模块(Symbol Timing Synchronisation)
最大 SNR 求解
假设输入信号码元 \(s(t)\) 的频谱密度函数为 \(S(f)\)
信道高斯白噪声 \(n(t)\) 的双边功率谱密度为 \(\mathbf{n}_{0}/2\)
滤波器的输入为:
\[
r(t)=s(t)+n(t),\quad\mathbf{0}\leq t\leq T_{\mathrm{B}}
\]
输出为
\[
y(t)=s_{0}(t)+n_{0}(t),\quad\mathbf{0}\leq t\leq T_{\mathrm{B}}
\]
其中,输出信号和输出噪声平均功率分别为
\[
s_{\scriptscriptstyle0}(t)=\int_{-\infty}^{\infty}\underline{{S_{\scriptscriptstyle0}(f)}}e^{j2\pi f t}d f=\int_{-\infty}^{\infty}\underline{{H(f)S(f)}}e^{j2\pi f t}d f
\]
\[
N_{0}=\int_{-\infty}^{\infty}{\frac{n_{0}}{2}}\cdot\left|H(f)\right|^{2}d f={\frac{n_{0}}{2}}\int_{-\infty}^{\infty}\left|H(f)\right|^{2}d f
\]
故得抽样时刻上的 SNR
\[
r_{0}={\frac{\left|s_{0}(t_{0})\right|^{2}}{N_{0}}}={\frac{\left|\int_{-\infty}^{\infty}H(f)S(f)e^{j2\pi f t_{0}}d f\right|^{2}}{{\frac{n_{0}}{2}}\int_{-\infty}^{\infty}\left|H(f)\right|^{2}d f}}={\frac{\left|\int_{-\infty}^{\infty}H(f)Y(f)\right|^{2}}{{\frac{n_{0}}{2}}\int_{-\infty}^{\infty}\left|H(f)\right|^{2}d f}}
\]
利用施瓦兹不等式
\[
\left|\int_{-\infty}^{\infty}X(f)Y(f)d f\right|^{2}\leq\int_{-\infty}^{\infty}\left|X(f)\right|^{2}d f\cdot\int_{-\infty}^{\infty}\left|Y(f)\right|^{2}d f
\]
找寻最大 SNR,即等号取得条件:
\[
X(f)=k Y^{*}(f)
\]
在本环境下,为
\[
H(f)=k S^{*}(f)e^{-j2\pi f t_{0}}
\]
线性共轭下达到 SNR 达到最大
\(H(f)\) 即为最佳接收滤波器的传输特性
此时有
\[
r_0\leq\frac{\int_{-\infty}^\infty\left|S(f)\right|^2df}{n_0/2}\quad\text{即 }r_0\leq\frac{2E}{n_0}
\]
即有
\[
r_{\mathrm{omax}}={\frac{2E}{n_{0}}}
\]
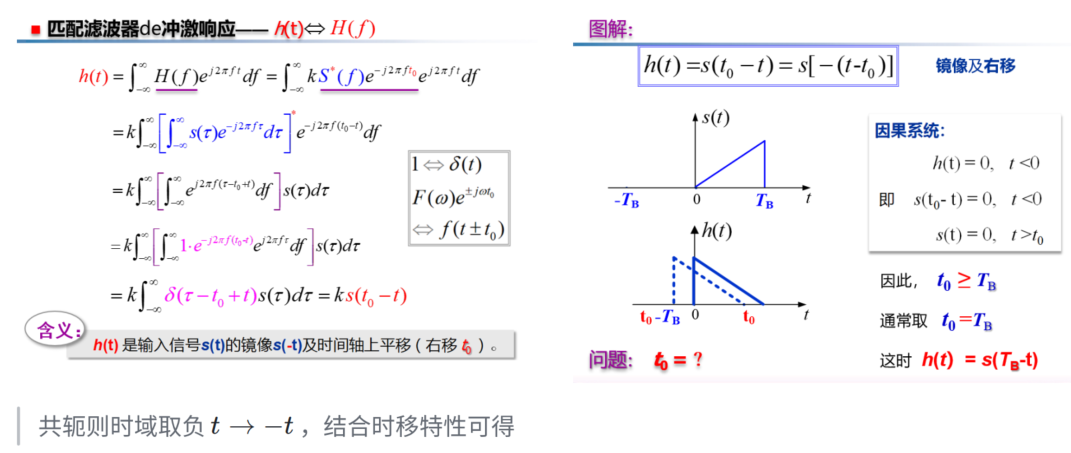
匹配滤波单位冲激响应
从性质分析,就是输入信号的反褶 + 位移
\(h(t)\) 是输入信号 \(s(t)\) 的镜像 \(s(-t)\) 及时间轴上平移(右移 \(t_{0}\) )
输出信号
输入信号与单位冲激响应的卷积
\[
\operatorname*{max}[s_{0}(t)]=s_{0}(t_{0})=R(0)=\int_{-\infty}^{\infty}s^{2}(t)d t=E
\]
匹配滤波的泛用性
只要信号能量 E 和噪声功率谱密度 n0确定,匹配滤波接收法适用于任何数字信号波形
- 也需要同步以采样到最大点
- 复数下为 \(h(t)=s^{*}(t_{0}-t)\)
例 | 求 h(t)、最大信噪比与输入波形
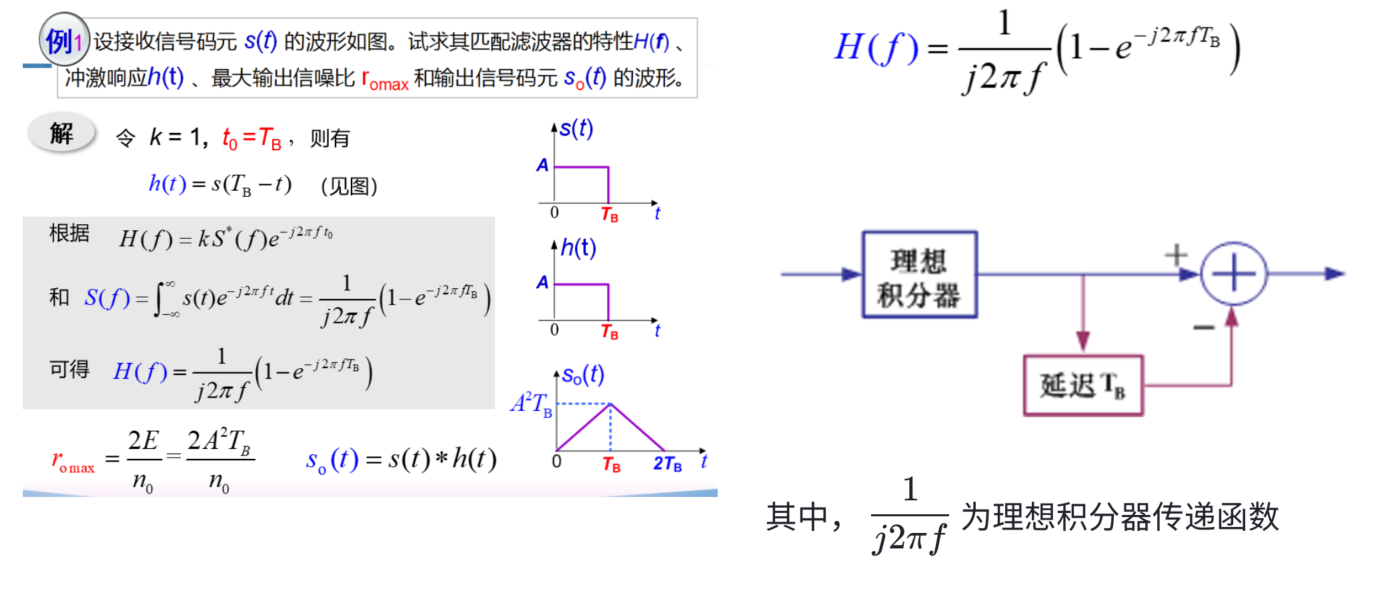
例
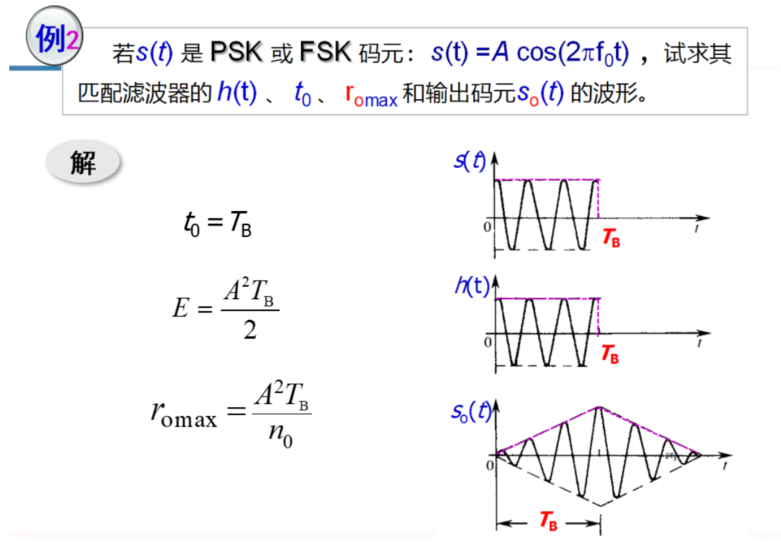
总结

最佳基带传输系统
即利用波形整形来匹配滤波
理想信道下的最佳基带系统
非理想信道下的最佳基带系统
信道噪声需要时域均衡